INDEX TO LECTURES

Astronomy 101/103 __________________________ Terry Herter

Lecture
Number		 Topic/Title Lecture
Number		 Topic/Title
1.
 The Universe: A very big place 11.
 Tools of Astronomy I
2.
 The Night Sky I 12.
 Tools of Astronomy II
3.
 The Night Sky II 13.
 Stellar Spectra
4.
 Perspectives: Learning the Language 14.
 Stellar Distances
5.
 Perspectives 15.
 The Properties of Stars
6.
 The Nature of Light 16.
 Energy Generation in Stars
7.
 Light and Atoms 17.
 Stellar Evolution
8.
 The Hydrogen Atom 18.
 Neutrons Stars & Pulsars
9.
 Blackbody Radiation 19.
 The Milky Way and Other Galaxies
10.
 Information from space 20.
 Normal and Active Galaxies

Lecture 1: Overview

Astronomy

The search unity of knowledge in our universe.

Some of the topics to be examined include:

  • Protostars & normal stars
  • Galaxies & quasars
  • The possibility of life on other worlds
  • White dwarfs, neutron stars & black holes
  • The origin and fate of universe

Course
Objectives

The objectives of this course are:

  • To learn astronomy
  • To understand and apply the scientific method
  • To practice critical thinking
  • To learn physics
  • To gain perspective about ourselves and planet eart

Scientific
Thinking

Scientific investigation is requires you to:

  • Ask questions: How, where, why, ...
  • Be objective
  • Use deductive and intuitive reasoning
  • Make quantitative calculations
Critical thinking involves revising your assumptions if they are wrong. The objective is not to prove a hypothesis, but to test the hypothesis.

Course
Philosopy

Our objective is to teach you astronomy not just about astronomy.

"Tell me and I will forget; show me and I may remember; involve me and I will understand."
- Chinese Proverb

Getting
Around
in Space

The velocity of light is the ultimate speed limit.

Velocity of Light =
 186,000 miles/sec
  300,000 km/sec

It is the fastest way for information to get to us.

Light
Travel
Times

Light can be a guage of how large space is. Let's look at the time it take for light to travel over different distances.

Earth-Moon 1 second
Sun-Earth 8 minutes
Sun-Pluto 6.5 hours
   
Sun-Alpha Centauri 4.3 years
Sun-Galactic Center 35,000 years
Sun-Andromeda Galaxy 2,200,000 years

The Light
Year

A light year is the distance travel in one year.

  • One light year (ly) = 9.5x1012 km

Traveling at 65 mph, it would take 10 million years to go 1 LY.

To travel to Alpha Centauri at this rate would take 44 million years!

No - A light year does not have half the calories of a regular year.

Scientific
Notation

Scientific notation allow representation of very small and very large numbers.

Examples of scientific notation are given below

0.001
 = 10-3
0.005
 = 5x10-3
0.1
 = 10-1
0.5
 = 5x10-1
1.0
 = 100
5.0
 = 5x100
100.0
 = 102
500.0
 = 5x102

What's
Out
There

The universe contains many types of objects. To name a few that we will discuss over the semester

  • Planets (and us)
  • "Stars"
    • Protostars, normal starts, red giants, white dwarfs, black holes, etc.
  • Interstellar clouds of gas and dust
  • "Galaxies"
    • Normal, radio, active
  • Quasars and ultraluminous galaxies

 

Lecture 2: The Night Sky - I

Lecture
Topics
Understand why the sky changes
  • During the night
  • From night to night

Some definitions

  • Celestial sphere, ecliptic, zodiac, zenith, meridian

SkyGazer demo


Sights
in the
Night
Sky
  • The Moon & Planets
  • Stars
    • Constellations
    • Asterisms (groupings of stars, for example The Pleiades)
    • Binaries
    • Variable Stars

Some sample objects are given in the table below. Click the link to get more information and see a picture.

OBJECT

EXAMPLE

Globular cluster

M13 in Hercules , M3, M15

Open cluster

h and c Perseus, Pleiades

Planetary Nebula

Ring Nebula (M57)

Galaxy

Andromeda (M31)

 

The
Need
to
Know

But Where to Look?

We need to know:

  1. Where an object is on the sky (coordinates or it location relative to some reference stars or constellations)
  2. What time that part of the sky is viewable, e.g. the sun is not up.
    • Time of night and
    • Time of year

Where
and
When
to Look
Consider the major motions that affect the night sky:
  • Rotation of the earth
    • Causes the stars to move through the sky at night.
  • Revolution of the earth around the sun
    • Causes different stars to be available at different times of the year.

The figure below demonstrates how different constellations are viewable at various times of the year. For instance, in winter Auriga and Orion are visible but Lyra and Hercules are hidden "behind" the sun. This situation reverses itself in the summer months.

Class
Demo
Cycles of the Sky

A class demo, wherein

  • the part of the sun is play by a volleyball
  • while the earth is played by a tennis ball and then a volleyball,
  • and the students are, of course, stars.

    (The prof. gets to play Atlas!)

Real Proportions

This table below give the relative sizes of the earth-sun system by relating them to everyday objects/distances.

OBJECT

EXAMPLE

If the sun were a volley ball

~ 8 in = 20 cm in diameter

The earth is small than a pea

~ 1.8 mm in diameter

sun-earth distance

22 m (about 71 feet)


The
Celestial
Sphere
  • The celestial sphere is the vast hollow sphere on which the stars appear fixed.
  • The celestial equator is defined by extending the earth's equator outward.
  • The N & S poles of the celestial sphere correspond to the earth's poles.

The
Ecliptic
  • The ecliptic is the apparent path of the sun through the sky.
  • It is also the plane of the earth's orbit about the sun on the celestial sphere.
  • Note: The ecliptic is tilted w.r.t. the earth's equatorial plane by 23.5 deg.

The
Zodiac
  • The zodiac is a band of celestial sphere that represents the path of the planets, the moon and the sun.
  • Extends ~8 deg to either side of the ecliptic.
  • In astrology the zodiac is divided into 12 equal parts called signs, each bearing the name of a constellation.

Astrology

Astrology is NOT a science!

  • Propagates the claim that a person's life is determined by the position of the sun, moon, and planets at birth.
  • This notion is patently false, and potentially harmful.
  • Astrology is neither a science nor a religion. It is probably better characterized as entertainment.
Zenith
and
Meridian

The zenith is the point on the celestial sphere that is directly above the observer.

The meridian is the great circle passing through the two poles of the celestial sphere and the observer's zenith.

 

Lecture 3: The Night Sky - II

Lecture
Topics
  • The changing sky (continued)
  • Using RA and Dec to find objects
  • In-class planetarium demonstration
  • Magnitudes
  • Fluxes and magnitudes

Equatorial
Coords

Astronomers use equatorial coordinates to locate objects on the celestial sphere.

Right Ascension (RA or a)

  • Equivalent to longitude
  • RA is measured in hours
    • The range is from 0 to 24 hours increasing on sky towards the east.
    • The "zero point" is towards the constellation Pices.

Declination (Dec or d)

  • Equivalent to latitude
  • Dec is measured in degrees.
    • The zero is on the equator
    • North Pole = 90 deg. , South Pole = -90 deg.

Notes:

  1. The equatorial (celestial) coordinate system is fixed on the sky.
  2. The coordinates of the stars and constellations do not change (ignoring precession).
  3. Since it is an "earth-centered" system the coordinates of the sun do change.

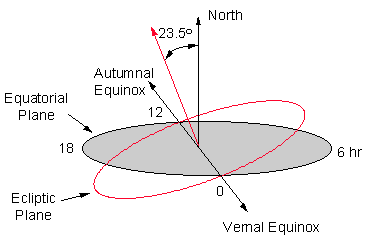
The diagram below illustrates the definition of RA along the equatorial plane and show the ecliptic plane and north celestial pole.


Equatorial
and
Ecliptic
Planes

The diagram below illustrates the definition of RA along the equatorial plane and show the ecliptic plane and north celestial pole.

Schematic showing ecliptic and equatorial planes


Equinoxes
and the
Seasons

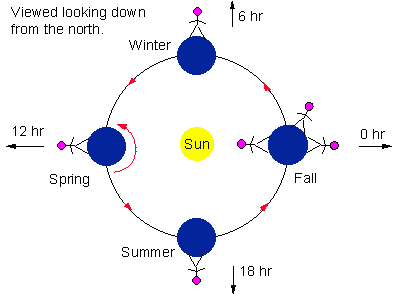
Definitions and the Seasons

The ecliptic intersects the equatorial plane at two locations, the vernal equinox (0 hr RA) and autumnal equinox (12 hr RA).

As the earth moves around the sun, the sun changes position in the sky relative to the background stars. Thus the RA of the sun changes every day.

For instance, on the first day of spring the sun is at the location of the vernal equinox, RA = 0 hr. On the first day of fall the sun appears in the direction of the autumnal equinox, RA = 12 hr.

The table below summarizes the location of the sun at the beginning of each season.

Event
Sun's RA
Comment
first day of spring

0 hr
Vernal Equinox
summer solstice
6 hr
first day of fall
12 hr
Autumnal equinox
winter solstice
18 hr


The
Fall
Sky

The figure below shows the location of the earth relative to the sun on the first day of fall. At local midnight an observer (for instance, you!) is standing on the opposite side of the earth from the sun and RA = 0 hr is crossing the meridian. Looking to the eastern horizon you see RA = 6 hr while looking to the western horizon you see RA = 18 hr.

RA = 0 hr on the meridian at midnight on Sep. 21.

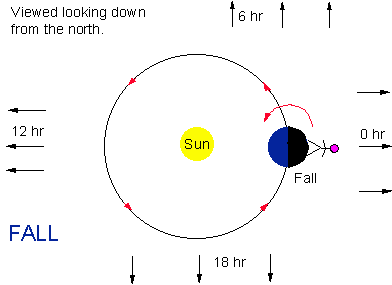
Fall Earth-Sun Diagram

The arrows indicate the direction of the celestial sphere of RA = 0, 6, 12, and 18 hr. Note that the earth is not located at RA = 0 hr in this diagram. The equatorial coordinate system is centered on the earth, so the RA and Dec of the earth have no meaning.

The
Revolving
Earth
The Revolving Earth and the Changing Sky

Since the earth revolves around the sun, at the same time each night, a different RA will be on the meridian at different times of the year.

For instance at midnight for the following dates, the RA's on the meridian are:

  • Sep. 21 ===> 0 hr
  • Dec. 21 ===> 6 hr
  • Mar. 21 ===> 12 hr
  • June 21 ===> 18 hr

The two figures below show "snapshots" of the sun-earth system on the first day of winter and spring.

RA = 6 hr on the meridian at midnight on Dec. 21.

Winter Earth-Sun Diagram

 

RA = 12 hr on the meridian at midnight on Mar. 21.

Spring Earth-Sun Diagram


The
Rotating
Earth

The Rotating Earth and the Changing Sky

As the earth rotates on its axis, the stars move through the sky over the course of a night. Like the sun, planets, and the moon, the stars rise in the east and set in the west due to the earth's rotation.

Consider the case illustrated below. At midnight, RA = 0 hr is on the meridian. As the earth turns, the observer moves. The graphic illustrates the location of the observer at 4:00 AM. Now RA = 4 hr is on the meridian and RA = 0 hr will appear west of the meridian to the observer.

On the first day of fall (Sep. 21), RA = 0 hr on the meridian at midnight. At 4:00 AM, RA = 4 hr will been on the meridian.

Fall Earth-Sun Diagram

Six months later on the first day of sping (Mar. 21), RA = 12 hr is on the meridian at midnight. At 4:00 AM, RA = 16 hr will been on the meridian.

Spring Earth-Sun Diagram


Summary
of the
Changing
Sky

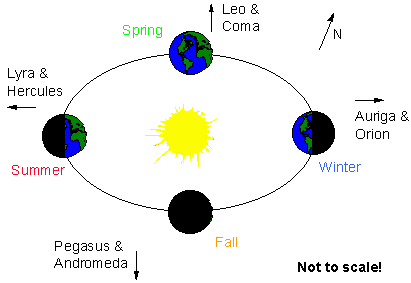
The figure below gives an overview of the different parts of the sky you can view different times of the year.

Overview Earth-Sun Diagram

All observers (people) are shown at local midnight, except for the fall where observers are shown at midnight, 4:00 AM, and noon.


Movement
of the
Sky

Your general knowledge tells you that objects (sun, moon, stars, etc.) rise in the east, cross the meriadian overhead, and set in the west.

Due to the revolution of the earth about the sun, these events happen earlier each successive night. Thus

  • Each night a given object will pass over the meridian 4 minutes earlier.
  • This corresponds to 2 hours earlier each month, or 24 hours in one year.
  • Objects rise and set earlier each day.

At a given time, the RA crossing the meridian increases by 4 min. per day.

Example 1: motion over the night

Suppose you see a star on the meridian at midnight. As you watch it, it moves to the west. So if you went out at 3:00 AM you would find the star west of the meridian. Likewise, if you had gone out earlier you would find the star east of the meridian.

Example 2: motion over several months

Suppose you observe a star on the meridian tonight at midnight. One month from now you go out to look at the sky at the same time. The star would now appear in the west. In fact, it would be "2 hours over" to the west. (Note that the sky at 2:00 AM tonight will be the same as the sky at midnight one month from now!)


Rotation
of the
Earth

RA = 0 hr on the meridian at midnight on Sep. 21. At 4:00 AM, RA = 4 hr will be on the meridian. As illustrated in the figure below this change is produced by the rotation of the earth.

 

Revolution
of the
Earth

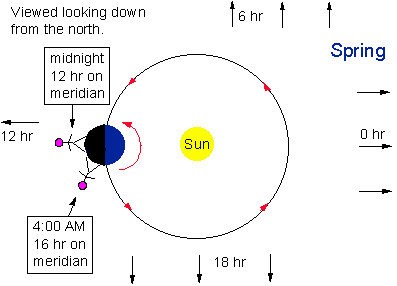
As illustrated below, when the earth has revolve around the sun by 180 degrees (6 months). There is a new view of the sky. RA = 12hr on the meridian at midnight on Sep. 21. At 4:00 AM, RA = 16 hr will be on the meridian.


Finding
an
Object

You can either know when the constellation an object is in is up or you can use the RA of the object to figure out when it is up. The first figure below illustrates the constellation approach while the second figure illustrates the RA approach.

Memorizing constellations and their availability is one way to tell when an object is visible.

Learning how to use an objects RA to determine visibility makes things much easier. (Although maybe not as much fun.)

Finding
Orion
On what date is Orion on the meridian at midnight? At 3:00 AM? At 9:00 PM?

For the Orion Nebula (M42), RA = 5.5 hr, Dec = -5.5 degrees

RA =6 hr transits at midnight on Dec 21.

  • => Orion transits at midnight on Dec 14.
Also
  • Orion transits at 3:00 a.m. on Oct. 31.
  • Orion transits at 9:00 p.m. on Jan 28.

Example 1

What RA is on the meridian at a given date and time?

What RA is on the meridian at 3:00 am on Feb. 21?

  • Dec. 21 -- 6 hr on meridian at midnight
  • Feb 21 -- 2 months later

    => add 4 hr
    => 10 hr overhead at midnight

  • At 3:00 AM => 3 hr later, 13 hr on the meridian

Example 2
On what day does a given RA cross meridian at a specific time?

A constellation is at RA = 14 hr. On what day will it cross the meridian at 9:00 PM?

  • When 14 hr crosses the meridian at 9:00 PM, 17 hr crosses the meridian at midnight.
  • On Mar 21: 12 hr crosses the meridian at midnight.
  • 17 - 12 = 5 hours

    => 2.5 months (10 weeks)
    => June 7

More on
Finding
Objects
  • Circumpolar objects can be visible any time of the year
    • Example: Polaris, the pole star.
  • Southerly objects are best observed during transit, that is, when they cross the meridian.

What's
up
Tonight?

What's "up" tonight?

  • Go to the A101/103 "Interesting Astronomy Sites" list for links to what's happening in the sky.
  • Observing suggestions
    • Best nights are when the Moon is absent.
    • Get away from city glare.
    • Get dark adapted (about > 20 minutes)
    • Use a "red light" to look at star charts/maps so you keep your night vision
  • Observing suggestions
    • Try to pick out some "easy" constellations such as the Big Dipper, the Little Dipper, Cygnus, and Cassiopea.
    • Planets follow close to the ecliptic (the path of the sun through the sky)
    • Remember, planets don't twinkle
  • We will discuss specific object to observe in class.

Magnitudes
  • We would like a way of specifying the relative brightness of stars.
  • Hipparchus devised a the magnitude system 2100 years ago to classify stars according to their apparent brightness.
  • He labeled 1080 stars as class 0, 1,.. 6.
  • 0 was the brightest, 1 the next brightest, etc.

Magnitude
Scale
  • The magnitude scale is logarithmic.
  • An increase in magnitude by 2.5 means an object is a factor of 10 dimmer, e.g.
    • A zero mag star is 10 times brighter than a 2.5 mag star.
    • A zero mag star is 100 times brighter than a 5 mag star.


Logarithms

Reminders about Logarithms

The table below list some sample base 10 logarithms.

Logarithm function

Power of 10

log (10) = 1

101 = 10

log (1) = 0

100 = 1

log (0.1) = -1

10-1 = 0.1

log (2) = 0.3

100.3 = 2

log (3) ~ 0.5

100.5 ~ 3

log (5) = 0.7

100.7 = 5

Note: If we have z = 10x, then x is the logarithm (base 10) of z. If z = ey then y is the natural logarithm (base e, e = 2.71828) of z. Base 10 logarithms are usually written as log10 or log, while nature logarithms are designated with ln.

Reminder: We have 10x * 10y = 10x+y. To multiply (divide) two numbers, add (subtract) their logarithms and take the anti-logarithm. In numerical terms, if x = log(A) and y = log(B) then C = A*B can be determined from C = 10x+y.

Sample
Magnitudes

The apparent visual magnitude of some of the brightest objects in the sky are given below.

Object

Apparent
Magnitude

Sun

-26.8

Full Moon

-12.6

Sirius

-1.47

Canopus

-0.72

Arcturus

-0.06

Betelgeuse

0.41


Magnitude
Limits
A dark adapted person with good eyesight can see to ~6th magnitude.

Hubble Space Telescope can observe objects at ~30 mag.

4x109 times fainter than the eye!

Observing
at
Night

Further suggestions on sky gazing

  • Go to a dark spot, away from city lights
    • Large city has 3.5 mag limit.
    • Country has 5.5 mag limit.
    • Mountains have 6.5 mag limit.
  • Get dark adapted (worth repeating)
    • This can take up to 45 minutes.
    • Use a "red light" to look at star charts/maps so you keep your night vision
  • Don't look directly at the object
    • Use averted or peripheral vision.

 

Lecture 4: Perspectives

Lecture
Goals

Review the basic physical vocabulary to describe:

  • How big, how tall, how fast, how massive, etc. ...

Understand terminology and learn the language.

Only then can you appreciate and understand astronomical concepts.

Basic Units

All physical quantities have units. The four basic ones we will use are:

  • TIME : seconds, hours, years, ...
  • DISTANCE : cm, m, light years, ...
  • MASS : gm, kg, ...
  • TEMPERATURE : Centigrade, Kelvin

Examples

Here are a few examples using units for time and distance.

Time  
1 yr =
 3.15x107 s
Lifetime ~
 2.5x109 s
   
Distance/Size  
Thumb =
2 cm = 0.02 m
Grain of sand =
 1 mm = 10-3 m
Atom =
10-10 m (1 A = 1 Angstrom)
Nucleus =
10-15 m (1 Fermi)
Diameter of Earth =
 12,800 km

Astronomical
Distances

Astronomers use a number of units to express astronomical distances. The most common ones are listed below.

 
 
    
Astronomical Unit
(AU)
 = 1.5x1011 m = Earth-Sun distance
Light year
(LY)
 = 9.5x1015 m = 63,240 AU
 Parsec
(pc)
 = 3.1x1016 m = 206,265 AU
       
 
1 PC
 = 3.26 LY  

Mass

Mass is a measure of the amount of matter in an object -- Not weight!

The mass of an object is the same on the earth or in space, but its weight depends upon gravity.

Here is a sample table that shows the difference between mass and weight.

Place
Mass
Weight
Comments
Earth
70 kg

154 lb.

size of a person

Moon
70 kg

26 lb.

1/6th gravity of earth

 Jupiter
70 kg

391 lb.

no solid surface

Sun
70 kg

2.1 tons

no solid surface

White Dwarf
70 kg

25,300 tons



So What?

Mass allows us to characterize an object independent of gravity.

  • Mass characterizes an objects "resistance" (inertia) to acceleration.
    • How hard it is to move an object or change its direction.

Temperature
  • Characterizes the internal motions of an object
  • Example: Air in a box
    • Particles (molecules) move faster when the temperature is higher.
  • There is a limit to how low temperatures can go -- absolute zero.
Absolute Zero is the limit to how low temperatures can go.

Temperature
Scales

There are a number of temperature scales. Astronomers use the one you are probably least familiar, the Kelvin or "Absolute Temperature" scale.

  • Celsius (Centigrade)
    • 0 C = Freezing point of water
    • 100 C = Boiling point of water
  • Kelvin
    • 0 K = Absolute Zero (-273.2 C)
    • K = C + 273
  • Fahrenheit: C = (5/9)*(F - 32)
    • The one most commonly used in the United States, but NOT used in the sciences.
    • Water freezes at 32 F and boils at 212 F.
It is somewhat amusing to note that the only place the Centigrade and Fahrenheit scale agree is at -40, that is, -40 F = -40 C.

Example
Temperatures

Like all units, any time you list a temperature indicate the scale you are using.

Object
F
C
K
Ithaca (July)
95

35

308

Ithaca (Feb)
-10

-23

250

Sun (surface)
9981

5527

5800

Pluto
-382

-230

43


Derived
Units
  • Originate from combinations of the basic units.
  • Used for convenience to let us speak more "simply" about things.
  • Some are:
    • velocity, acceleration, angles, and density
    • force, pressure, energy, and power
    • luminosity

Velocity
and
Acceleration
Examples
  • Velocity
    • Walking: 3-5 mph = 1.3-2.2 m/sec
    • Sprinter: 25 mph = 11 m/sec
    • Velocity of earth around the Sun:   30 km/sec
  • Acceleration
  • Ex: 0 to 60 mph in 10 seconds => 2.7 m/sec2
  • Ex: Earth gravity accelerates objects at 9.8 m/sec2

Angular
Size
and
Density
Examples
  • Angular size
    • Moon & Sun: 30 arcminutes
    • Jupiter: 30 to 49 arcseconds
    • Pluto: ~ 0.1 arcsecond
    • Resolution of the eye: ~1 arcminute

    Your thumb at arms length subtends an angle of about 3 degrees.

    [Your thumb is about 2.5 cm (1 inch) wide. Extending your arm your thumb will be about 50 cm from your eye.]

 

Density

Density represents the mass (or number of particles) per unit volume of a substance, material, or object.

Densities can vary greatly between materials (e.g. lead vs. gold vs. aluminum) and states of matter (e.g. liquid vs. gas).

Some Example Densities

Material

Mass Density
(g/cm3)

Particle Density
(particles/cm3)

Water

1

3.7x1022

Lead

11.3

3.3x1022

Gold

19.3

5.9x1022

Air

1.3x10-3

3x1019

Space

2x10-24

1


Density
and
Mass

If a body is of uniform density then mass = density x volume.

Examples

  • 1 gallon (3.8 liters) of water:    
    • mass = 3.8 kg => 8.4 lb.
  • 3 x 4 x 8 inch (96 in3) bar of gold is 30 kg

Force

Force: F = m*a or a = F/m

  • A force is that which can change the velocity of an object (either speed or direction).
    • 1 dyne = g-cm/s2
    • 1 Newton = kg-m/s2 = 105 dynes = 0.2248 lb
      • Named after Isaac Newton
  • Forces cause acceleration.
  • Example Forces
    • Friction (Electromagnetic Force)
    • Gravity
      • Earth's gravity: 980 g-cm/sec

A Poem
  • by Jack Prelutsky about Energy and Power

    "The Turkey Shot out of the Oven"

 

Lecture 5: Perspectives/Cosmic Forces

Lecture
Goals
  • Conclude Perspectives Discussion
    • Pressure, Energy, Power, Luminosity
  • Discuss properties of matter
    • Atoms, Isotopes, and Molecules

Pressure
Pressure = force/area
  • 1 Pa = kg/(m*sec2) = N / m2 (after Blaise Pascal)
1 atmosphere
= 14.7lb/in2
  ~100 kPa
  = 1 bar
  = 760 mm Hg (mercury)
  = 29.92 inches Hg

Pressure
Examples

Pressure depends not just upon the force but also the area. A small force can produce a large pressure if the contact area is small. An ordinary needle penetrates objects because of the small area of the tip - thus it is easy to generate high pressures.

Some examples are given below.

50,000 Pa:
 Pressure on the floor of a 50 kg person in ordinary shoes
5x106 Pa:
 Pressure on the floor of a 50 kg person in high heels
5x106 Pa:
 Pressure on the highway from a 5 ton truck

Energy
Energy: force*dist
  • The capacity for doing work.
    • Kinetic: Energy of motion (KE)
    • Potential: Stored energy (PE)
  • Units of Energy
    • 1 Joule (J) = N-m (after James Joule)
    • 1 erg = dyne-cm = 10-7 J
    • 1 calorie = 4.186 J
    • 1 kilocalorie = 1 Calorie (nutrition)

Energy
Examples

Some everyday and not so everyday example of energies.

8.4x106 J
 = 2000 Calories
= Energy the body uses in one day
330,000 J
 = energy to boil 1 quart of water
= energy to run a 60 W light bulb for 1.5 hours
400,000 J
 = energy of a 1 ton car at 60 mph
 
  
1 erg
 = a snow flake hitting the ground
1000 J
= energy a match produces
4x109 J
 = 1 ton TNT
1015 J
 = nuclear explosive (250 kilotons TNT)
1025 J
 = solar flare

Power
Power: energy/time
  • The rate at which energy is used (or work is done).
    • Watt (W) = 1 Joule/sec = 107 ergs/sec
  • Examples
    • 1 kW/m2 = Solar power hitting the earth
    • 100 W = Rate at which the body expends energy
    • 100 W light bulb - only 1/5 of power goes into light, the rest goes to heat

Luminosity

Luminosity is the power radiated by an object (energy/sec).

Total Energy radiated by an object of constant luminosity is given by:

  • Total energy = Luminosity x Lifetime

People
Example
A person radiates ~ 100 W.

So that the energy output in a day is


Object
Energetics

In many cases the luminosity of an object is quoted in solar luminosities. Below is a table that will help make some connection to from (large) earth based to galaxy size luminosities.

Object

Luminosity
(Watts)

Total Lifetime
Energy Output
(Joules)

Nuclear bomb

1021

1015

Solar Flare

1023

1025

Star

1026

1044

Supernova

1037

1044

Milky Way

1037

1055


Units are
a Must

Using Units for Calculations

  • Always use units.
    • Can't understand the answer without them.

  • Check if an answer makes sense:
    • Are the units correct?
    • What "order of magnitude" do you expect for the answer

Prefixes
for Units

Some Example Densities

Name

Symbol

Factor

Length
Example (meters)

Giga

G

109

109

Mega

M

106

106

kilo

k

103

103

centi

c

10-2

10-2

milli

m

10-3

10-3

micro

m

10-6

10-6


Atoms
  • Atom => "indivisible"

  • Matter is made of atoms.
    • Very small particles in constant motion.
    • About 1024 atoms in your thumb

  • Different atoms => different elements

Simple
Picture of
an Atom
A simple picture consists of a nucleus made up of protons and neutrons surrounded by a cloud of electrons.


Simplest
Atoms
Hydrogen and helium are the simplest, lightest atoms in the universe.

  • Hydrogen: Most abundant and simplest atom

  • Helium: Next most abundant element
The schematic atoms above are not to scale!

Properties
of Atoms
  • Atoms are intrinsically neutral
    • # protons = # electrons
  • Atoms are small and mostly space.
    • Size of nucleus = 10-15 m
    • Size of atom = 1 x 10-10 to 2 x 10-10 m
  • If a nucleus were 1 mm in size then the electrons would be over 100 m away!
Note: Atoms consist of mostly empty space!

Other
Atoms

A few additional example atoms are given below:

  • Carbon - important for life
    • 6 p+, 6 n, 6 e-
  • Iron - most stable element
    • 26 p+, 30 n, 26 e-
  • Uranium
    • 92 p+, 146 n, 92 e-
    • Heaviest naturally occurring element.
    • radioactive - unstable

 


Isotopes

Isotopes of an element have the same number of protons, but a different number of neutrons.

For example:

  • U-238: 92 p+, 146 n, 92 e-
  • U-235: 92 p+, 143 n, 92 e-

 

Molecules
  • Chemically combined atoms
  • Example -
    • Water: H2O
    • 2 Hydrogen atoms and 1 Oxygen atom
  • Electrons are shared between the H-atoms and the O-atom.

 

Lecture 6: The Nature of Light

Lecture
Goals

Cosmic forces (forces of Nature)

  • The four fundamental forces (Gravity, E-M, Strong, and Weak)
  • GUTs and TOEs

Light

  • Wavelength and Frequency
  • The E-M Spectrum
  • Light and Energy

Forces of
Nature

The four fundamental forces of nature are:

Force

Relative Strength

Comment

Nuclear

1

Holds nuclei together

Electromagnetic

1/137

Holds atoms, molecules, our bodies, etc. together

Weak

10-13

Responsible for radioactive decay of certain particles

Gravitational

10-39

Holds planets together, governs evolution of the universe, etc.

Your everyday experience is with Electromagnetic and Gravitational Forces.


E-M
Forces
  • Allows us to exist (among other things).
  • Hold us together, make blood flow, make molecules form, etc.
  • Very strong
The EM force can be either attractive or repulsive
Unlike charges attract
(+)==>
 <==(-)
Like charges repel
<==(+)
 (+)==>
<==(-)
 (-)==>

Light

What is light?

Light is an electromagnetic (EM) wave propagating through space.

EM waves (photons) include:

  • ultraviolet radiation
  • visual light
  • infrared radiation
  • radio waves, etc.
Aside [In case you are interested]:

Light is a transverse wave. This means that the oscillation is perpendicular to the direction of motion (much like a water wave).

So what causes light to exist and move? In physics it is known that a changing magnetic field causes a changing electric field (and visa versa). A photon consists of a time varying electric and magnetic field which regenerate each other! As far as we know this will go on forever unless the photon gets absorbed (by an atom or collection of atoms).

 

The Colors
of Light

Isaac Newton determined that when light passes through a PRISM (see below), it disperses into various "colors".

In essence, he used a PRISM to make a rainbow, and invented spectroscopy.

"Nature and nature's laws lay hid in the night:
God said, 'Let Newton be!' and all was light."
... Alexander Pope

 

Spectroscopy

Spectroscopy breaks the light into different (wavelengths) colors.

Rain drops act as prisms to cause a rainbow.


Wavelength
of Light

Light is characterized by a wavelength, which is the distance between two similar points in the wave, e.g. the valleys or peaks.


Frequency
of Light

In addition to wavelength, we sometimes talk about the frequency of a photon.

Let "c" be the speed of light (3x108 m/s), then we have

Relationship between frequency and wavelength
l f = c or f = c/l
where
  
f
 = frequency of radiation
l
 = wavelength of radiation
c
 = speed of light
What is "frequency"?
  • If a wave goes by while you are sitting in a boat, you go up and down at a given rate.
  • This is the frequency of the wave.
  • The analogy carries over to light waves.

The E-M
Spectrum

The electromagnetic spectrum is our "window" to the Universe. Historically various parts of the E-M spectrum have been given labels. Some of the most common names are listed below.

Radiation

Approximate Wavelength

 

Angstroms

Microns

Gamma rays

0.01

10-6

X-rays

1

10-4

Ultraviolet

1000

0.1

Visible

5000

0.5

Infrared

105

10

Microwave

107

103

Radio

108

104

Radio

109

106


Why the
Labels?

The use of labels is partly for convenience and partly historical.

Photons of different energy are usually detected with different instruments.

  • our eyes detect visible light
  • radio detect radio waves

Light
and
Energy

Just like particles, photons carry energy. Each wavelength has a unique energy given by the expression below (Einstein again!)

Let "c" be the speed of light (3x108 m/s), then we have

Relationship between energy and frequency/wavelength
where
  
h
 = Planck's constant
 
 = 6.626x10-34
f
 = frequency of radiation
l
 = wavelength of radiation
c
 = speed of light

Long waves, such as radio waves, carry little energy.

Short waves, like X-rays, carry lots of energy.

This is why ultraviolet radiation can give you a sunburn and cause cancer (see the discussion on the ozone hole below).

Atmospheric
Windows

Atmospheric windows are locations in the EM spectrum where the atmospheric is transparent.

The atmosphere only allows certain wavelengths to pass through it.

  • Visible: 3500 - 10000 A
  • Radio: 1 mm - 100 m

This is one reason why astronomers want observatories in space.


The
Ozone
Hole

Ozone (O3) occurs at an altitude that varies with latitude and season. The peak concentration in the ozone layer occurs at about 16 km. However, ozone is present up to about 80 km.

Because it has an absorption band near 3000 A, ozone blocks the ultraviolet (UV) rays from the sun. Due to their shorter wavelength (higher frequency), UV photons have more energy than their optical counterparts. This means that they can damage our skin, potentially resulting in cancer.

A breakdown in the ozone layer can not only be harmful to humans but plant and animal life as well.

Aside [In case you are interested]:

At shorter wavelengths absorption due to water, atomic and molecular oxygen, and atomic and molecular nitrogen blocks UV and X-rays from reaching the earth.

 


Forces of
Nature
(Again)

The four fundamental forces of nature are:

Force

Relative Strength

Comment

Nuclear

1

Holds nuclei together

Electromagnetic

1/137

Holds atoms, molecules, our bodies, etc. together

Weak

10-13

Responsible for radioactive decay of certain particles

Gravitational

10-39

Holds planets together, governs evolution of the universe, etc.

Your everyday experience is with Electromagnetic and Gravitational Forces.


Gravity
Newton formulated his theory of gravity in 1667

More mass => stronger attraction

Newton's law of gravity is given by:

F =

Force of attraction (Newtons)

G =

6.67 x 10-11 m3kg-1sec-2

m1 , m2 =

masses (kg)

d =

distance between objects (m)

In words, this means that the attractive force between to bodies is proportional to the produce of their masses. The more massive a body the stronger the attraction.

In addition the force gets weaker as you move the bodies further apart. It decreases as the square of the distance. Doubling the distance means the force is four times weaker.

Gravity
Examples

The table below (column 4) shows how much more you would weigh if you were standing on the "surface" of the various astronomical bodies.

Examples of Surface Gravity

Object

Mass
(Earth=1)

Diameter
(Earth=1)

Gravity
(Earth=1)

Moon

0.0123

0.27

0.17

Venus

0.81

0.95

0.91

Mars

0.11

0.53

0.38

Jupiter

317

11.2

2.54

Sun

333,000

109

27.9


Aside [In case you are interested]:

These numbers are derived from Newton's law of gravity and the force equation F = ma. We typically designate the acceleration due to gravity with the letter g, thus a = g. Let your mass (or what every object you want) be m and the mass of the planet or star be M. Then g = F/m = GM/d2 gives the gravity. Rather than looking up the value of G, the gravitational constant, you can compute everything relative to the earth (mass, diameter, and gravity). This is done for the table above.

 

Nuclear
Force
  • Holds atomic nuclei together
  • Glues protons and neutrons together
  • Very short range
  • Can release tremendous amount of energy via fusion or fission
    • Nuclear energy
    • Atomic bomb

Energy
and
Matter
E = mc2

Einstein showed there is an equivalence between mass and energy.

1000 kg of matter converted into energy

    => 9x1019 J

    = total energy consumption of the U.S. in one year

Energy
from
Fusion

Fusion is the combination of two or nuclei to form a heavier nucleus.

For example, fusing Hydrogen into Helium releases energy by the conversion of mass (since He is less massive than H).

    4 H -> He + 4.2 x 10-12 J

Example chemical reaction

    2H + O -> H2O + 1.5 x 10-19 J

Fusion releases about a million times more energy per reaction.


Nuclear
Fission

Fission is the breaking up of nuclei

Uranium fission:

    U235 + n -> Ba141 + Kr92 + 3n + energy

Hiroshima Atomic Bomb

    10-20 kg of U235
    ~ 1 kg achieved fission
    ~ 15,000 tons of TNT in explosion
    Total bomb weight ~ 4000 kg

Energy
Release

Energy from Fusion and Fission

Energy is released when elements lighter than iron are fused together. Likewise energy is released when element heavier than iron are split apart (fission). Conversely, to fuse heavier elements or split light elements requires extra energy.

The plot below shows the "binding energy" per nucleon versus mass number. Iron is the most tightly bound nucleus. This means that moving towards iron releases energy. It is like a ball rolling to the lowest point.

Binding energy of atomic nuclei

Weak
Force

The Weak Force is responsible for the radioactive decay of certain kinds of particles.

The decay of the neutron is an example of the weak interaction.

n --> p + e- + n

The neutron decays into a proton, electron, and a neutrino (actually an antineutrino). The neutrino is very low (perhaps zero) mass particle that interacts very little with matter.


Unified
Theories

The "standard model" of particle physics brings together quantum chromodynamics (QCD) and electroweak theory. QCD describes the strong (force) interactions under the hypothesis that all strongly interacting particles are made of quarks. The electroweak theory unifies the weak and electromagnetic interactions. Together general relativity and the "standard model" appear to explain all known physics.

Unified Theories attempt to bring together our understanding of physics one step further.

Grand Unified Theories (GUTs)

  • The strong, weak, and electromagnetic interactions are unified.
  • GUTs have the basic idea that these three forces are really manifestations of one force. [If we could do experiments at very high energies (1014 to 1015 GeV) then there would be one force, not three.]
  • However, even the simplest GUTs have over 20 free parameters (such as the charge of the electron) that must be determined experimentally.
  • The ultimate GUT would have only a few or perhaps no adjustable parameters.

Theory of Everything (TOE)

  • The idea behind a TOE to include gravity as well.
  • This would unifies all 4 forces, and perhaps create a theory in which there are fewer adjustable parameters.
  • This hasn't been done yet

TOEs

The tree below shows the hiearchical structure for GUTs and TOEs.

 

Lecture 7: Light and Atoms


Lecture
Topics
  • Spectroscopy
    • The Colors of Light
  • The Bohr model of the atom
  • Quantum Mechanics
    • Determinism
    • The Uncertainty Principle
    • Quantum numbers in atoms
    • Energy Levels in atoms

Origin
of Light
Where Does Light Come From?

The following had been known during the 19th century:

  • accelerated charges produce light
  • and hence emit energy

If we picture an electron as in orbit around the nucleus, it should radiate light

  • changing direction is acceleration! (a force is required from something to change direction)
Aside [In case you are interested]:
Radio stations broadcast via a tower in which electrons move up and down. This oscillation causes E-M (radio) waves which carry away energy and form the signal which you pick up on your radio.

Problems
in
Paradise
This caused a major problem w/ classical physics

If the electron radiated due to its motion around the nucleus, it would lose energy and soon spiral into the nucleus.

The world should collapse instantly!

  • Fortunately it doesn't.

So what is wrong with this picture?

Enter Quantum Mechanics (QM)

The
"New"
Physics

Quantum Mechanics was developed during the revolution which occurred in physics from 1900 - 1930.

Both Special Relativity and General Relativity were developed during this time.

Bohr Model
of the Atom

In 1913, Niels Bohr formulated 3 rules regarding atoms:

1. Electrons can only be in discrete orbits.

Bohr
Model

2. A photon can be emitted or absorbed by an atom only when an electron jumps from one orbit to another.


Bohr
Model

3. The photon energy equals the energy difference between the orbits.

The photon energy is E = hf = hc/l since c = lf, and f = c/l, where E is the energy difference between the two orbits.

About
Quantum
Mechanics
General Facts
  • The discrete (quantum) nature of the energy "levels" of the electron gives QM its name.
  • QM describes the microscopic world.
    • Physics of the small
  • There are some very non-intuitive things associated with it.
Determinism in QM
  • Classical physics is deterministic.
  • That is, a given cause always leads to the same result.
  • Even chaotic behavior is deterministic.
  • However, in quantum mechanics this is not the case!
QM: The Uncertainty Principle
  • The uncertainty principle of QM states that we cannot know both where something is and how fast it is moving.
  • Thus we cannot predict exactly what will happen in a given experiment.
  • We can only give the probability of an outcome.
  • The more accurately you measure the position the less accurately you know the velocity and vice versa.

Particle-Wave
Duality
  • Atomic particles (electrons, protons, etc.) sometimes behave like particles and sometimes like waves.
  • Photons can do this too!

Example:

An example of particles behaving like waves is interference. You have probably seen the wakes from two different boats "interfere" on the water. In some cases they enhance one another (constructive interference) while at other times they cancel one another (destructive interference). Photons do this but so can particles!

Small
to
Big

The microscopic world of atoms and electrons

    leads us to ...

the super-macroscopic world of stars and galaxies.

Comment: Why do we care about the very small? It is the very small that make up stars and galaxies. These microscopic constituents give us information about the composition, temperatures, velocities, and more.


Quantum
Numbers

Quantum Numbers (Q.N.) specify the "location" of an electron in an atom.

An electron can reside in one of many orbits.

  • n = number of orbits = Principal Q.N.
  • n = 1 is the lowest energy state.
  • If n > 1, then the atom is "excited."

Atomic
Energy
Levels

For convenience, instead of drawing circular orbits in which the energy is high for each successive orbit, we draw an "Energy Level Diagram" as shown on the right below. The energy levels of an atom are now represented by horizontal lines. Energy increases as you move upward in the diagram.

Electronic
Transitions

An electronic transition occurs when a electron moves between two orbits.

When absorption of a photon occurs, an electron goes up, e.g. from n=1 to n=2.

Emission of a photon occurs when an electron moves down, e.g. from n=2 to n=1.

The
Quantum
Stepladder

An analogy to the energy levels in the atom is the "Quantum Stepladder" where the rungs on the ladder correspond to energy levels in the atom.

Spectra
from
Atoms

A spectrum is the intensity of light seen from an object at different wavelengths.

  • e.g. done by spectroscopy with a prism.

Individual atoms, like H, show spectral lines, i.e. For H, these are the Balmer lines in the visible.


Hydrogen
Balmer
Spectrum

A schematic representation of the spectrum of hydrogen in the visible is shown below.

 

Lecture 8: The Hydrogen Atom

Lecture
Topics

The Spectrum of Hydrogen

21-cm Emission from Hydrogen

Ionization of atoms

Learn how these emissions and absorptions are useful to astronomy.

  • Each element, ion, or molecule has a unique signature
  • These signatures are the Rosetta Stone of Astronomy

The Spectrum
of
Hydrogen

Hydrogen has one electron, so it is the simplest of the elements in terms of its spectrum.

Like other elements Hydrogen has discrete emission or absorption lines which result when the electron move between energy levels.

  • Note, to move "up" a level, a photon of exactly the correct energy (or wavelength) is required.

The Hydrogen atom can emit and absorb light at discrete wavelengths in the ultraviolet, visible, infrared, and radio.

In the visible the lines are called the Balmer lines.


Hydrogen
Balmer
Spectrum

A schematic representation of the hydrogen Balmer spectrum is show below.
Hydrogen
Energy
Levels
The energy level diagram for hydrogen is given below. The various hydrogen spectral "series" are defined by their ending (bottom) level, e.g. for the Lyman series all electronic transitions go to level one, while for the Balmer series all electrons go to level two.

Hydrogen Spectral Lines

Aside (In case you are interested)
There are names for series where the electron goes to levels 3, 4, 5, or 6 that are respectively called the Paschen, Brackett, Pfund and Humphreys series.

Energy

The energies in atoms are usually expressed in electron volts (eV).

  • 1 eV = 1.6 x 10-19 J

For instance, the energy difference between n=2 and n=1 in H is 10.2 eV.

Since E = hc/l, l = 1216 A

Aside (In case you are interested)
The electron volt is defined as the work required to move an electron through a potential difference of 1 volt. In "electrostatics" the force on a charged particle is given by F = q E, where q = charge and E is the electric field strength. For a uniform electric field, V = E d where V is the electric potential (measured in volts) and d is the distance moved (note that the electric field has units of volts/meter). Then we have Energy = F d = q V.

Hydrogen
Spectral
Lines

The spectral lines in the ultraviolet are call the Lyman series. In the visible these are called the Balmer series.

Series

Designation

Transition
(Levels)

Wavelength

Lyman (UV)

     

Lya

2-1

1215.7 A


Lyb

3-1

1025.7 A


Lyg

4-1

972.53 A


...

   

limit

infinity-1

911.5 A

Balmer (visible)

     
 

Ha

3-2

6562.8 A

 

Hb

4-2

4861.3 A

 

Hg

5-2

4340.5 A

 

...

   
 

limit

infinity-2

3646.0 A

"Transition" indicates the change in energy level (designated by the principle quantum number) of the electron. For instance, 3 - 1 implies the electron falls from n = 3 to n = 1 in the atom.

The term "limit" indicates the limit to reach the continuum (see below). If a photon has more energy than this threshold (shorter wavelength) it can ionize hydrogen.


Spectral
Line
Notes

Key Features of the Atoms

The energy levels get closer together as the quantum numbers get larger.

The greater the difference between the quantum numbers, the larger the energy of the photon emitted or absorbed.

The
Continuum

If an electron is given enough energy (via a photon or by other means) it can escape the atom. The electron is then "unbound" and the quantization of energy levels disappears.

  • An electron in the continuum has escaped from the proton.

  • The energy of an electron in the continuum is not quantized.

The continuum is shown schematically in the energy level diagram below, above the n = infinity principle quantum number. Photons with energy exceeding 13.6 eV can promote the electron into the continuum -- freeing the electron from the hydrogen atom.

Hydrogen Spectral Lines


Hydrogen
21-cm
Radiation

An important spectral line in astronomy for measuring the gas between stars is the 21-cm line of Hydrogen.

  • This is in the radio part of the spectrum.
The n = 1 level (ground state) of H is actually "split" into 2 levels separated by a very small energy.
  • This splitting is due to the fact that the electron and proton have intrinsic spin, i.e. they behave like small magnets.
  • When the North poles are aligned the energy is higher than when they are not.

The figure below illustrates the "spin flip" that cause the emission of a 21-cm photon.

A 21-cm photon is emitted when poles go from being aligned to opposite (a spin flip).

This emission from a small number of H-atoms is very weak, but hydrogen is very plentiful in space.

  • So we see a lot of 21-cm radiation from our galaxy.
Ionization
and
Ions

If a photon has enough energy, it can ionize an atom, i.e. promote an electron into the continuum.

An atom becomes an ion when one or more electrons have been removed.

Though adding an extra electron also creates an ion, it is much more difficult and rare.

Many atoms in space are ionized. Fortunately each ion has its own spectral signature.

Hydrogen
Ionization

The ionization energy of hydrogen is 13.6 eV.

Ionizing an electron from the ground state (n = 1) of hydrogen requires photons of energy 13.6 eV or greater.

=> l < 912 A

Ionized hydrogen is just a proton by itself!


Helium
Ions

All elements can be ionized by removing one or more electrons. The example of helium is shown below.

It takes progressively more energy to remove successive electrons from an atom.
  • That is, it is much harder to ionize He II than He I.

Note: You can not have He IV!


Notation

Astronomers use the following notation to indicate the ionic state of an atom.

Suffix
Meaning
Examples
I
neutral
He I, O I
II
once ionized
He II, O II
III
twice ionized
He III, O III
IV
three times ionized
O IV, Ne IV

Spectral
Signatures

Spectral Signatures: Astronomy's Rosetta Stone

The set of spectral lines associated with a given ion are unique and are of fundamental importance to astronomy.

We call this the "spectral signature" of an ion.

Allows the identification of elements across the galaxy and universe.

  • With spectral signatures we can identify oxygen, carbon, iron, etc.

In addition these signatures provide information on:

  • Chemical composition of the stars
  • Abundances of the elements
  • Physical conditions of the gases such as densities and temperatures

Emission
from
Solids

Solid materials have a continuous spectrum rather than a discrete one.

This is different from individual atoms.

Examples:

  • Tungsten filament light bulb - continuous
  • Fluorescent lamp - discrete

 

Lecture 9: Blackbody Radiation

Lecture
Goals

Learn some diagnostics associated with detecting radiation.

  • Kirchhoff's laws

Heat and Energy Transfer

Learn about blackbody emission.

  • Properties
  • Wien's law
  • Stephan-Boltzmann law

Energy Flux

Luminosity

Kirchhoff's
Laws
  • These are three laws, know as Kirchhoff's laws, that govern the spectrum we see from objects.
  • They allows us to interpret the spectra we observe.

1. A hot solid, liquid or gas at high pressure has a continuous spectrum.

There is energy at all wavelengths.

Kirchhoff's
Laws

2. A gas at low pressure and high temperature will produce emission lines.

There is energy only at specific wavelengths.

Kirchhoff's
Laws

3. A gas at low pressure in front of a hot continuum causes absorption lines.

Dark lines appear on the continuum.

Types
of
Spectra

As illustrated below, Kirchhoff's laws refer to three types of spectra: continuum, emission line, and absorption line.

Thus when we see a spectrum we can tell what type of source we are seeing.

Heat
Transfer
  • All objects radiate and receive energy.
    • In everyday life, we call this heat.
  • The hotter an object, the more energy it will give off.
  • An object hotter than its surroundings will give off more energy than it receives
    • With no internal heat (energy) source, it will cool down.

Energy
Transfer

There are three ways to transport or move energy from one location to another:

  • Conduction:
    • particles share energy with neighbors
  • Convection:
    • bulk mixing of particles, e.g. turbulence
  • Radiation:
    • photons carry the energy

Internal
Energy
of
Objects
  • All objects have internal energy manifested by the microscopic motions of particles.
  • There is a continuum of energy levels associated with these motions.
  • If the object is in thermal equilibrium, it can be characterized by a single quantity, it's temperature.

Radiation
from
Objects
  • An object in thermal equilibrium emits energy at all wavelengths.
    • resulting in a continuous spectrum
  • We call this thermal radiation.

Blackbody
Radiation
  • A black object or blackbody absorbs all light which hits it.
  • This blackbody also emits thermal radiation. e.g. photons!
    • Like a glowing poker just out of the fire.
  • The amount of energy emitted (per unit area) depends only on the temperature of the blackbody.

Planck's
Law
  • In 1900 Max Planck characterized the light coming from a blackbody.
  • The equation that predicts the radiation of a blackbody at different temperatures is known as Planck's Law.

Note that the peak shifts with temperature.


Blackbody
Properties
  • The peak emission from the blackbody moves to shorter wavelengths as the temperature increases (Wien's law).
  • The hotter the blackbody the more energy emitted per unit area at all wavelengths.
    • bigger objects emit more radiation


Wien's
Law

The wavelength of the maximum emission of a blackbody is given by:

Some sources of radiation and the wavelength of their peak emission are given below.

Object

T (K)

lpeak (mm)
lpeak (A)

Sun

5800

0.5

5000

People

310

9

90000

Neutron Star

108

2.9x10-5

0.3


Impact
of
Wien's
Law

Consequences of Wien's Law

Hot objects look blue.

Cold objects look red.

Except for their surfaces, stars behave as blackbodies.
Blue stars are hotter than red stars.

Stefan-
Boltzmann
Law

The radiated energy increases very rapidly with increasing temperature.

where s = 5.7x10-8 W m-2 K-4.

For instance, when T doubles the power increases 16 times: 24 = 2 x 2 x 2 x 2 = 16. Likewise if T triples the power increases by 81 times.

Energy
Flux

The Energy flux, F, is the power per unit area radiated from an object.

The units are energy, area and time.

Luminosity

Total power radiated from an object.

For a sphere (like stars), the area is given by: Area = 4pR2 (m2)

So the luminosity, L, is:

You can see the dependencies on radius and temperature.

Examples:

  • Doubling the radius increases the luminosity by a factor of 4.
  • Doubling the temperature increases the luminosity by a factor of 16.

Worked
Example
# 1

Suppose I observe with my telescope two red stars that are part of a binary star system

Star A is 9 times brighter than star B.

What can we say about their relative sizes and temperatures?

Since both are red (the same color), the spectra peak at the same wavelength. By Wien's law

then they both have the same temperature.

By our law governing Luminosity, radius, and temperature of an object (star!)

It must be that star A is bigger in size (since it is the same temperature but 9 times more luminous). How much?

Star A is 9 times more luminous:

So, Star A is three times bigger than star B.

Worked
Example
# 2

Suppose I observe with my telescope two stars, C and D, that form a binary star pair.

  • Star C has a spectral peak at 350 A (0.35 mm, deep violet)
  • Star D has a spectral peak at 7000 A (0.70 mm, deep red)

What are the temperatures of the stars?

By Wien's law

Thus we have for star C,

and for star D

If both stars are equally bright (which means in this case they have equal luminosities since the stars are part of a pair the same distance away), what are the relative sizes of stars C and D?

Now we have

So that stars C is 4 times smaller than star D.

 

Lecture 10: Information from Space

Lecture
Topics
  • The Doppler Effect
  • Luminosity
  • Brightness (flux)
  • Distance

Doppler
Effect

The Doppler Effect is a change in the observed frequency of light due to relative motion. Only the motion along the line-of-sight matters.


Water
Waves

Water Wave Illustration

Consider Suppose you are traveling a boat and encounter a "water wave" generated by the wake of another boat. The speed at which you transverse the wave will depond upon whether you are traveling with or againt the wave.

Boat moving into waves
  • When the boat is traveling into the waves, the peaks hit the bow more rapidly than if the boat were standing still.
Boat moving away from waves
  • Likewise, when the boat is traveling away from the waves, the peaks hit the rear less rapidly than if the boat were standing still.

Sound
Waves

Sound wave exhibit the Dopper effect.

  • The frequency of sound waves increases as a source approaches the observer, and decreases as it recedes.

You may have noticed this happens when a car or train passes by you. There is a change in pitch between the car is approaching and the car receding.

E-M
Waves

Electromagnetic Waves - Light

  • The Doppler effect also modifies light (photons).
  • Because atoms emit light at discrete frequencies, we can detect their motion (velocity) by a "shift" in frequency from the expect one.

Emission
Lines

Spectral Line Reminder

According to Kirchhoff's laws, a hot, low pressure gas will have an emission line spectrum.

Emission Line Spectrum

Frequency
Shift

Shifts in Frequency (and wavelength) for Moving Sources

When sources are in motion relative to the observer the spectrum shifts to the blue or red because of the Doppler effect. This change can be easily seen because the wavelength shift of the spectral lines is are easy to see.

Shifting spectral lines

Blueshift
and
Redshift

Astronomers use the shortcut terms blueshift and redshift to refer to the direction (or sign) of the Doppler shift.

Approaching sources

  • Spectral lines shifted to higher frequencies
  • => short wavelengths.
  • Spectrum is blueshifted

Receding sources

  • Lines move to lower frequencies
  • => longer wavelength
  • Spectrum is redshifted

Calculating
the
Spectral
Shift
The Doppler Shift Quantified

The change in wavelength is proportional to the velocity.

Delta lambda/lambda = v_r/c

where vr is the radial velocity

  • positive velocity => receding
  • negative velocity => approaching
Note: This formula is only valid for low velocities. The velocity of an object can never exceed the speed of light, but the Doppler shift can become infinite. As v approaches c, the wavelength increases to infinity.

Example
Doppler
Calculation

Doppler Shift Example

In a star, the Balmer line H-alpha is observed at a wavelength of 6565 A. What is the star's radial velocity? (H-alpha rest lambda = 6563 A.)

Star is receding from us. (longer lambda)

v_r = (2A/6563A)*3x10^5 km/sec

So vr = 91 km/sec.

Importance
of Doppler
Effect

Importance of Doppler Effect

The Doppler effect is very important because it is the only way of measuring the motions of distant objects.

As we shall see later, the Doppler effect allowed Edwin Hubble to deduce that the universe was expanding, and serves as a means to find the distances to distant galaxies.

Luminosity
and
Flux

Luminosity and Flux

Here we review the definitions of some important quantities that we will use often in the course.

Luminosity, L, is the total energy radiated from an object per second.

  • Measured in Watts

Energy flux is the flow of energy out of a surface.

  • Measured in Watts/m2

The observed flux (apparent brightness) of an object is the power we receive from it.

  • Depends on the distance to the object.
  • Measured in W/m2

We often just use the term flux without the "energy" or "observed" qualifier. The unspecified qualifier is determined by the context.

Inverse
Square
Law

How is the Observed Flux determined?

Make a sphere of radius, r, around an object which is radiating power.

  • Such as the sun or a light bulb

All energy radiated from the object must pass through this sphere

  • The size of the sphere does not matter!

However, the flow of energy per m2 passing through the sphere decreases as the size of the sphere increases.

The flux of energy through the sphere is

f = L/(4*pi*r^2)

r = radius of sphere

L = luminosity of the object

This formula is called the Inverse Square Law because of the dependence on the radius of the sphere.

The radius of the sphere is just the distance to the object.


Why do
we care
about the
Flux?

The flux is what we measure.

We use a telescope (or our eye) and measure a small fraction of the light passing through this sphere.


Example
Inverse
Square
Law
Application

An Illuminating Example?

A 100 W light bulb
  • about 1/5 of power goes into light

It's total power output is always 100 W.

It's apparent brightness to us depends upon how far away it is.

If we double the distance away from the light bulb, the flux drops by a factor of 4.

Avoiding
Flux
Confusion

Confused About Flux?

To reiterate, here are the definitions and usage of energy and observed flux.

Energy flux: F = sigma*T4 (W/m2)

  • Energy flow out of the surface of a star (or any object).

Observed flux: f = L/(4*r2) (W/m2)

  • Apparent brightness
  • Energy flow through a sphere of radius r due to a star (or any object) of luminosity L.
  • Inverse square law behavior
 

Relating
Fluxes

Observed and Energy Flux are Related

The luminosity of a star is L = 4pR2 sT4

The total power is energy flux times area.

So for a star with radius R and temperature T.

What
to
Know
You should be able to use the inverse square law to determine how the apparent brightness (observed flux) of an object changes with distance

For example, doubling the distance decreases brightness by factor of 4

You should know that luminosity scales as R2T4 and be able to use this information

For example, doubling size increases luminosity by factor of 4, or

doubling temperature increases luminosity by factor of 16


Distances
from the
flux

Measuring Distance!

If we know the luminosity of an object (such as a star) and measure the flux --

r = sqrt( L/(r*pi*f) )

we can determine its distance!


Standard
Candles

Objects with known luminosity are called standard candles in astronomy.

They are of fundamental importance.

Astronomers use standard candles to measuring distances.

There are very few standard candles and it is a problem to calibrate them (determine L).

 

Lecture 11: Tools of Astronomy - I

Lecture
Topics

Telescopes

  • How we gather light

Devices for detecting photons

  • How we collect light

Angular Resolution

  • Resolving fine details

Telescopes

What is a telescope?

  • It is an instrument that collects and focuses light (onto a photon detector!)

Why do we build them?

  • To make much more sensitive observations
  • To resolve small details on the sky

Telescope
Types

There are two basic classes of telescopes, refracting and reflecting.

Refracting

  • Focuses light through a lens
    • e.g. a camera lens or
    • a magnifying glass

Reflecting

  • Focuses by reflecting light off a mirror
    • e.g. a shaving mirror

Refracting
Telesopes

Refracting telescopes use a large lens to gather and focus light.

Origins: The practical form of the refractor emerge between 1608 and 1610 in Italy and Holland. Hans Lippershey(1570-1619), born in Wesel, Germany was a Dutch spectacle maker who developed a practical telescope and applied for a patent in 1608. Pisa-born Galileo Galilei (1564-1642), upon hearing of the invention of the telescope, built his own. He used it to do astronomy discovering the moons of Jupiter, the phases of Venus, structure on the Moon, sunspots, and stars too faint for the eye to see.

Problems
with
Refractors

There are three basic problems with refracting telescopes.

  1. Must make a large piece of glass with no defects (bubbles, impurities, etc.).
  2. Must suspend the heavy glass by the rim
  3. Chromatic aberration
    • Different wavelengths of light are bent differently (like a prism!).
    • Largest refractor is ~1 meter in diameter.

Reflecting
Telescopes

Reflecting telescopes reflect light from an aluminized, curved mirror to a focus.


Mirror
Shape

The mirror always has the shape of a conic section: a parabola, hyperbola, or ellipse.

Cassegrain
Telescope

The diagram below show the elements and optical path for a Cassegrain Telescope. A secondary mirror reflects the light back through a hole in the primary mirror. Cassegrain telescopes are relatively compact.

Nicolas Cassegrain (1625-1712): A Frenchman who invented the two mirror telescope shown here. Almost all modern optical telescopes follow this form.

Newtonian
Telescope

Isaac Newton (1643-1727): An Englishman who made the first useable reflector and invented the telescope that bears his name. The secondary in this case is a flat mirror. This telescope has been the favorite of amateur astronomers because of its ease of construction. However, it tends to be long and the location of the eyepiece can be inconvenient.

Contrary to popular belief, Newton did not invent the reflecting telescope, but he did make the first one.

Reflector
Advantages
Advantages of Reflecting Tel's
  • Light is reflected off the surface so it doesn't pass through the material.
  • Can support from the back.
  • No chromatic aberration (all light is reflected equally).

Gathering
Light
What a Telescope Does -
  • "Gathers up" the "flux" from an object.
  • The amount of light (or power) collected depends upon the area of the telescope mirror.
  • Thus, bigger telescopes are better
    • They collect more light

Eye
vs.
Telescope
  • A dark adapted eye has diameter D ~ 7 mm.
  • Mt. Palomar telescope: D = 5 m.
  • It collects

times more light!
  • Thus you could see much fainter with it.

Limiting
Magnitude
How Faint Can You Go?
  • Looking through the Palomar telescope, you should see about 14 mags fainter
    • i.e. 20th magnitude
  • But Palomar observes objects much, much fainter than this (~25th mag).
  • How does it do this?


Photon
Detectors
  • Photon detectors are devices which respond to E-M radiation.
  • Photographic film detects photons
    • Used in the "olden" days of astronomy
  • Today "solid state" detectors are used, e.g. CCD's (charge-coupled devices)
    • Used in low-light level camcorders and electronic cameras


Detectiing
other Parts
of E-M
Spectrum

Other Wavelengths

  • Solid state photon detectors in one form or another are used to detect radiation across the E-M spectrum.
  • Earlier, photographic covered a very limited portion of this spectrum:
    • visible, UV and X-ray
    • But was not very efficient
      (only detecting 1 photon in about 20)

Integration
Time
  • Integration time is the exposure time of the detector.
  • The dark adapted eye integrates photons for ~1/8 to 1/4 second.
  • CCDs can integrate for hours.
  • The long exposure time means many photons can be collected from the source.

Angular
Resolution
  • Angular resolution is the ability to distinguish between nearby objects.
  • Measured in arcseconds or arcminutes.
  • The eye has a spatial resolution of ~1 arcminute.

Angular
Resolution
Quantified

The angular resolution, theta, of a telescope is given by:




where lambda = the wavelength and D = telescope diameter

Resolution
in the
optical
and
Radio

Some numbers

  • Optical wavelengths (lambda ~ 5000 A)


  • Radio wavelengths (1 mm to 100 m)

Notes
on
Angular
Resolution
  • Larger telescopes have better angular resolution.
  • However, it is the size of the telescope relative to the wavelength that counts.
  • Radio telescopes need to be very large to get "good" angular resolution.

Atmospheric
Blurring
  • Telescopes are placed on mountain tops to get better seeing (thinner air).
  • But atmospheric blurring limits the angular resolution ~0.5 arcsec (5000 A).
  • Adaptive optics corrects the blurring due to the atmosphere in real time
  • Uses a deformable mirror
  • Developed for the military

 

Lecture 12: Tools of Astronomy - II

Lecture
Topics
  • Interferometers
  • Where to put your telescope
  • Telescopes around and above the world

Interferometers
  • Interferometry synthesizes a larger diameter telescope with a set of smaller telescopes spaced a large distance apart.
  • Achieves high angular resolution roughly equal to the largest telescope spacing.

Schematic Interferometer

Simple Interferometer Picture


Schematic Radio Telescope

A schematic view of a radio telescope is shown below. Key component are the primary mirror (or dish), the secondary mirror, and the receiver.

Simple Picture of a Radio Telescope

An operating radio telescope is shown below.

This is an 25-m, 240 ton radio telescope located in Fort Davis, Texas. It is part of the VLBA network (see below). You can find pictures of all the VLBA antennas which are located across the United States at the VLBA website.

Features of Interferometers
  • Advantage: Cheap to build compared to a single large telescope.
  • Disadvantage: Most photons hit the ground between the dishes.
  • Thus interferometers give excellent angular resolution but are much less sensitive than a single "filled aperture" telescope would be.

Radio Interferometers

Most interferometry is done in the radio.

The Very Large Array (VLA)
  • 27 radio dishes, each 25 m in diameter spaced in a Y pattern which is 20 km along each leg.
  • Simulates a 40 km diameter telescope
  • At 2 cm the angular resolution is about 0.1"
    • Could see a dime in Elmira!

Above is a picture of the VLA. This picture and others can be found at the VLA web site. Click on the "What is the VLA?" link and go to photographs of the VLA.

The Very Long Baseline Array (VLBA)

  • 10 radio dishes, 25 m in diameter located across the world from Hawaii to the Virgin Islands.
  • The baseline is about 8,000 km.
  • The resolution at 2 cm is ~0.0003" !!
    • Could "split a hair" in Elmira!

Telescope Summary
  • Reflecting telescopes are the best.
  • Larger telescopes collect more photons => larger is better.
  • Angular resolution: theta ~ lambda / D
    => larger is better
  • Interferometry allows a large aperture to be simulated.

Below is a list of some telescopes from around the word. You can click on the names to get to an observatory web page. Most have public informtion areas.

Name
Size (m)
Wavelength Measured
Location
Palomar*
5
Visible/IR
S. Calif.
MMT
6.5
Visible/IR
Arizona
Gemini
2 x 8.1
Visible/IR
Arizona/Chile
VLT
4 x 8.2
Visible/IR
Paranal, Chile
Keck
10
Visibl/IR
Hawaii
AST/RO
1.7
Submm Radio
Antarctica
JCMT
15
Submm Radio
Hawaii
IRAM
30
mm Radio
Spain
Nobeyama
45
mm Radio
Japan
Effelsberg
100
cm Radio
Germany
GBT
100
cm Radio
Greenbank, WV
Arecibo*
300
cm Radio
Puerto Rico
VLA
27, 25
cm Radio
N. Mex.
VLBA
10, 25
cm Radio
N. Hem.
*Cornell affiliation

Telescope
location

Where To Put Your Telescope

  • Everyone (astronomers anyway) wants one, but not all locations are equal.
  • Put on barren mountain tops
    • For best "seeing"
  • Keep away from big cities
    • Avoid light pollution
  • But not always enough!
    • -- Ain't no mountain high enough!


Transparency
of the
Earth's
Atmosphere
Simple Interferometer Picture


Wavelengths
of
Light

Why Do We Care to Observe at all These Wavelengths?

At different wavelengths, we see different objects:

Wavelength
Characteristic Object
Gamma-Ray
Compact object which collapsed
X-Rays
Neutron stars
Ultraviolet
Hot stars, quasars
Visible
Stars
Infrared
Red giant stars, galactic nuclei
Far-IR
Protostars, dust, planets
Millimeter
Cold dust, molecular clouds
cm Radio
HI 21-cm line, pulsars

 

Getting Rid of the Atmosphere
  • On the surface of the Earth, only a few parts of the spectrum are transparent (mostly in the visible and mm-cm radio). The rest are opaque.
  • In the visible, we are plagued by the turbulence in the atmosphere -- seeing.
  • Put telescopes above the atmosphere!
    • Eliminates "seeing" as a problem.
    • Gets above the absorbing atmosphere.
  • Possibilities
    • Airborne Observatories
    • Balloons
    • Spacebased observatories

Space --
The New
Frontier

Some Observatories and Wavelength Bands

  • Past
    • Einstein: X-ray
    • IRAS (Infrared Astronomical Satellite)
    • GRO: Gamma Ray Observatory
    • ISO: Infrared Space Observatory
  • Present
    • Hubble Space Telescope: UV, Optical
    • AXAF: Advanced X-ray Facility
  • Future:
    • SIRTF: Space Infrared Telescope Facility (2002)
    • NGST: Next Generation Space Telescope (2006?)

 

Lecture 13: Stellar Spectra

Lecture Topics
    • What is a star?
    • Emission from Stars
    • Stellar Spectra

Stars?

What is a Star?

  • Stars "shine" at night.
  • A star is a self-luminous sphere of gas.
  • It is held together by gravity.
    • But what keeps it from collapsing?
      (More on this later)

 

The Spectra
of Stars
A telescope with a spectrograph measures the spectrum of a star and gives the brightness at different wavelengths.
    • Like we discussed with blackbodies.
  • Almost all stars show a "continuum" spectrum with "absorption" lines.
  • Some stars show "emission" lines.
    • All stars do not have the same spectrum!

Spectra of Blackbodies


Spectra --
  • Almost all stars show a "continuum" spectum with "absorption" lines.
  • Some stars show "emission" lines.
  • All stars do not have the same spectrum!

    Schematic Spectra of Star


Continuum Spectrum
  • Despite having absorption lines, the spectrum of a star is close to that of a blackbody.
  • What we see is produced by the hot surface called the photosphere.
  • For the Sun:
    • Photosphere is ~ 100 km deep
    • T ~ 6000 K

Stars as Blackbodies
  • If stars are similar to blackbodies, then the spectrum will be close to Planck's law.
  • => Spectrum will have a peak
  • With Wien's law (lambdapeak = 2900 microns/T) we can estimate the temperature.


Stellar Spectra

  • The spectral (absorption) lines we see in stars are very important.
  • The "missing" photons give us info on:
    • Chemistry
    • Temperature
    • Density
  • Kirchhoff's laws tell us about the region which gives rise to the spectrum.


Formation
of Stellar
Spectrum


Hydrogen
Balmer
Spectrum

The hydrogen Balmer spectrum is visible for most stars.


Classification of Stars

In the late 19th century astronomers catagorized stars according to the strength of the hydrogen absorption lines in the spectrum.
  • They labels these A, B, ... from strongest to weakest.
  • Unfortunately, this was the wrong way to do it!

Annie Jump Cannon arranged the spectra of stars in a sequence which corresponds to their temperatures (She classified over 500,000 stars in her career!)

  • The spectral sequence is:
    • O, B, A, F, G, K, M
    • Hotter to cooler (A temperature sequence)
For more information and pictures on Annie Jump Cannon visit: http://cannon.sfsu.edu/~gmarcy/cswa/history/pick.html

 


Classification of Stars...


  • Each of these classes (O, B, etc.) can be subdivided into tenths, i.e.
    • G0, G1, ... G9, K0, K1, ... K9
      (G0 is hotter than G9)
  • The Sun is a G2 star.

More pictures and information on spectral sequences can be found at:
http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit1/sptypes.html


Changes
to the
Spectral
Sequence
  • For the first time in over 100 years the spectral sequence is in need of another letter.
  • Very low temperature stars discovered with infrared surveys of the sky.
  • Now an L and T stars have been added!

O, B, A, F, G, K, M, L, T

Stellar
Photometry
and
Colors
  • It is not necessary to measure the entire spectrum to determine the spectral peak of a star.
  • We can use color filters to determine the "colors" of a star.
    • By this we mean how much flux is seen in each color filter.
    • A green filter transmits only green photons.


      The UBV system:

  • A set of color filters which give coarse spectral information.


Temperature
and Colors
  • U at 3500 A => ultraviolet
  • B at 4300 A => blue.
  • V at 5500 A => visible
  • A hot star will have more flux in the U filter than the V filter compared to a cool star.

Colors of a Hot Star vs. a Cool Star

 

Lecture 14: Stellar Spectra & Distances

Lecture
Topics
  • Stellar Spectra
    • The classification of stars
  • The Distances to Stars
    • How far to the stars
    • Stellar Parallax

Spectral
Sequence = Temperature Sequence

The Spectral Sequence

  • A figure of the spectral sequence to be inserted here (when I find a good one - see your textbook for now) - see the link below from some sample spectra.

 

More pictures and information on spectral sequences can be found at:
http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit1/sptypes.html

Absorption Line Information


Temperature
Absorption Lines
High
Ionized atoms
Intermediate
Neutral atoms
Low
Molecules


Strength of Lines vs.
Spectral Class

 

Stellar Spectral Sequence

 

Class
Temperature (K)
Features
Examples
O
28000-60000
He II, Si IV, O III
Orionis
B
10000-28000
He I, Si II, H I
Rigel, Spica
A
7500-10000
H I, Fe II, Mg II
Sirius, Vega
F
6000-7500
Neutral metals, Fe I,

weak H I and Ca II
Canopus,

Polarius
G
5000-6000
Ca II, Neutral metals
Sun, Capella
K
3500-5000
Neutral metal,

Mol. Bands, TiO
Arcturus, Aldebaran
M
<3500
Mol. Bands, TiO,

VO, Neutral Metals
Betelgeuse,

Antares

 

The Picture
is Not Yet
Complete
  • The spectral type (class) of a star gives us temperature information, but we don't know its luminosity.
  • To get the luminosity, we must know the distance!
  • Remember the inverse square law!

Stellar Distances
  • How do we measure distances to nearby stars?
  • Astronomers use the parallax method.
  • The method is similar to that used by surveyors.

Surveyor's
Method

Observing the object from points A and B, we can compute the distance to it from angles alpha and beta, and the length of the baseline.


Stellar
Parallax






A nearby star will change position on the sky relative to distant (background) stars.


Calculating
Distances

How Do We Calculate Distances?

We have a very skinny triangle on the sky.

Determining Distances

  • Parallax is measured in arcseconds.

Notes on
Parallax:
  • As stars get further away, their parallax becomes smaller.
  • Parallax can not be measured to better than ~0.02" from the ground (d < 50 pc).
  • Alpha Cen has the largest parallax (~0.8")
  • 1 pc = 3.26 ly (light-years)

Current
Status
  • The satellite Hipparcos has measured the parallax of 120,000 stars to better than 0.002".
  • => d < 500 pc
  • Data still being worked.


Parallax
Distances

Importance of Parallax Distances

  • Parallax is the key to knowing distances in the universe.
  • Nearby stars are the stepping stones to measuring the distances to everything else in the universe.
  • We can now compute the luminosity of stars!

 


L, f and d
  • The luminosity, brightness (flux) and distance are related by the inverse square law:
  • Knowing the brightness and the distance, we can compute L.

Example:

  • A star like the sun has an observed flux of 2.4x10-10 W/m2. If the flux of the sun at the Earth is 1 kW/m2, how many parsecs away is the star?

  • There are two ways to work it:

Method 1: Calculate Lsun directly

  • Lsun = 4 x 3.14 x (1.5 x 1011 m)2 x 1000 W/m2 = 3 x 1026 W

  • dstar = sqrt ( 3 x 1026 W / (4 x 3.14 x 2.4x10-10 W/m2 )) = 3 x 1017 m = 10 pc

    • Method 2: Proportions

     


    The Closest
    Stars


    Star
    Parallax (")
    Distance (pc)
    Luminosity (Lsun=1)
    Proxima Centauri
    0.763
    1.31
    5 x 10-5
    a Centauri A
    0.741
    1.35
    1.45
    a Centauri B
    0.741
    1.35
    0.40
    Barnards Star
    0.522
    1.81
    4 x 10-4
    Wolf 359
    0.426
    2.35
    2 x 10-5
    Lalande 21185
    0.397
    2.52
    5 x 10-3
    Sirius A
    0.377
    2.65
    23
    Sirius B
    0.377
    2.65
    5 x 10-3

     


    Comparing
    Stars

    • If all stars were at the same distance, it would be easy to compare their properties.
    • But we can:
      • Find stellar distance.
      • Use the inverse square law to find what it's brightness would be at a standard distance.

     

    Absolute
    Magnitude
    • Astronomers adopt 10 pc as the standard distance.
    • The brightness a star would have at this distance is its absolute magnitude (Mv).
    • This is an intrinsic property of the star!
    • This differs from apparent magnitude (mv) which is how bright a star appears in the sky.

     


    Apparent
    and
    Absolute
    Magnitude

    Relating Apparent (mv) and Absolute (Mv) Magnitude

    • Suppose a star has mv = 7.0 and is located 100 pc away.
    • It is 10 times the standard distance.
    • Thus, it would be 100 times brighter to us at the standard distance.
    • Or 5 magnitudes brighter
    • => Mv = 2.0

     


    The Distance Modulus
    Equation
    • The relation between mv and Mv is written in equation form as:
      • mv - Mv = - 5 + 5 log10( d )

        where d is in parsecs.
    • mv - Mv is called the distance modulus.

    Examples

    • Deneb: mv = 1.26 and is 490 pc away.
      • mv - Mv = - 5 + 5 log10( d )
        1.26 - Mv = - 5 + 5 log10( 490 ) = -8.5
        => Mv = -7.2
    • Sun: mv = -26.8, d = 1 AU
      • -26.8 - Mv = - 5 + 5 log10( 1/206265 )
        => Mv = 4.8

     

     

    Lecture 15: Stellar Properties

    Lecture
    Topics
    • Stellar Magnitudes
      • Review
    • The Hertzsprung-Russell Diagram
    • Luminosity Classes of Stars
    • Binary Stars

     

    The Distance Modulus
    Equation
    • the relation between mv and Mv is written in eqation form as:

      mv-Mv=5+5 log10(d) where d is in parsecs.

    • mv-Mv is called the distance module

      Examples
    • Deneb: mv=1.26 and is 490 pc away. mv-Mv=-5+5 log10(d) 1.26-Mv=-5+5 log10(490)=-8.5 =>Mv=-7.2
    • Sun: mv=-26.8, d=1AU -26.8-Mv=-5+5 log10(1/206265) =>Mv=4.8

    Bolometric Magnitude
    • The absolute bolometric magnitude is the brightness at ALL wavelengths.
    • Usually represented by M.
    • Mv is the absolute visual magnitude.

    Magnitude
    Summary
    • mv = apparent magnitude
      • apparent visual brightness of a star in the sky
    • Mv = absolute magnitude
      • visual brightness the star would have if it were at 10 pc
    • M = bolometric magnitude
      • total brightness (over all wavelengths) a star would have if it were at 10 p

    Luminosity
    vs.
    Color of Stars
    • In 1911, Ejnar Hertzsprung investigated the relationship between luminosity and colors of stars in within clusters.
    • In 1913, Henry Norris Russell did a similar study of nearby stars.
    • Both found that the color (temperature, spectral type) was related to the luminosity.

    Schematic
    Hertzsprung-Russell
    Diagram


    Observational Effects
    • An H-R diagram of the brightest stars will preferentially show luminous stars since we can see them further away.
    • An H-R diagram of the nearest stars show many M type stars since M stars are very numerous.

    Absolute
    Magnitudes

     

    Notes on H-R Diagram
    • There are different regions
      • main sequence, giant, supergiant, etc.
    • Most stars lie along the main-sequence.
    • For a given spectral class (e.g. K), there can be more than one luminosity.
      • i.e. main-sequence, giant or supergiant
    • On the main sequence, there are many more K and M stars than O and B stars.


    Luminosity
    Classes
    • Ia : Brightest Supergiants
    • Ib : Less luminous supergiants
    • II : Bright giants
    • III : Giants
    • IV : Subgiants
    • V : Main-sequence stars

    Luminosity Classes


    Luminosity
    • Total energy per second radiated from a star of radius R.
    • The luminosity, L, is given by:

    • So supergiants must be big!!

    How Big
    are
    Supergiants?
    • Betelgeuse: M2 Iab (supergiant)
      • L ~ 40,000 Lsun, T ~ 3,500 K
    • Sun: G2 V (main-sequence)
      • T ~ 5,000 K

     

    H-R Diagram Showing Radii of Stars


    Spectorscopic
    Parallax
    • From a star's spectrum, we can determine its spectral and luminosity class.
    • Given the star's apparent brightness (observed flux), we can then estimate its distance.
    • This distance determination technique is called spectroscopic parallax.

    Spectroscopic Parallax Example

    • Observe a G2 Ia star (supergiant) which has
      • mv = 10 (apparent magnitude)
    • The absolute magnitude (from the H-R diagram) is Mv = -5.
    • How far away is the star?
    • but mv - Mv = -5 + 5*log10(d)
      => log10(d) = 20/5 = 4
      => d = 10,000 pc


    Setellar
    Properties

    • What do we know about stars?
      • temperature
      • luminosity
      • radius
      • composition
    • All we need now is the mass.


    Stellar
    Masses

    • The mass of a star is very important in determining its properties.
    • The mass and composition are all you need to know about a star!
      • determine the temperature, radius, and luminosity of a star over its lifetime.
    • But, how do we "weigh" a star?
    • Binary stars
      • pairs of stars that orbit each other
      • used to determine masses of stars


    Binary Stars


    Types of
    Binaries
    • Visual Binary
      • Stars are separated in a telescope.
    • Spectroscopic Binary
      • See two sets of spectral lines Doppler shifted due to orbital motion.
    • Eclipsing Binary (rare)
      • Stars cross in front of one another.


    Binary Stars
    Importance

    • 75 % of all stars are "binary stars"
    • Studies give:
      • Stellar Masses (Visual & Spectroscopic)
      • Stellar Radii (Eclipsing)

     

    Lecture 16: Energy Generation in Stars

    Lecture
    Topics
    • Conclusion of star formation
    • What makes stars shine
      • Possible energy sources
      • Fusion
    • Energy Transport in stars

    T Tauri
    Stars
    • Named after the first one found.
    • Newly formed stars which are just clearing away the surrounding material.
    • Surface eruptions, rapid variations of light output and mass loss via "wind".
    • Many are surrounded by disks!!
      • Could planets be forming there?
    • Sun was probably once a T Tauri star.

    What makes
    the Sun
    Shine
    The Sun emits 4x1026 Watts
    • People power on the earth is about 600 billion Watts
    • US Power consumption is about 1013 Watts
    • Equivalent to > 100 billion nuclear bomb/sec

    We know from dating of rocks on the Earth and Moon that the Sun is at least 4.5 billion years old.

    • => Need about 6x1043 J of energy

    Energy
    Sources

    Possible Energy Sources for Main Sequence Stars

    • Chemical Reactions
      • Such as a burning fire
      • ==> Sun's lifetime ~ 1000 years!!
    • Gravitational Compression
      • Shrinking - use gravity, like a water fall
      • Must collapse ~50 feet per year!
      • ==> Sun's lifetime ~ 15x106 years.
    • Nuclear reactions
      • Convert mass to energy
      • Much more energy per unit mass than chemical reactions


    Mass
    to
    Energy
    • Albert Einstein - 1905
      • Equivalence between mass and energy
        E = mc2
    • Main-sequence stars release energy by converting Hydrogen into Helium
      • 4 H1 ==> He4 + energy
      • Superscript is number of protons + neutrons.

    E = mc2

    4 H1 ==> He4 + energy

    • mass of 4 H1 = 6.693x10-27 kg
    • mass of 1 He4 = 6.645x10-27 kg
    • The mass difference is released as energy
      • ~0.048 x10-27 kg per reaction
    • E = mc2 = 0.048x10-27 kg x (3x108 m/sec)2
      • E ~ 4.3 x 10-12 Joules
      • Energy is created out of mass!
    • Converting the hydrogen into helium for the Sun would produce about 1044 J of energy
      • Enough to keep the Sun burning for about 10 billion years

    Fusion
    and Fission
    • Fusion is the process of creating heavier elements from lighter ones.

      e.g. 4 H1 => He4 + energy

    • Fission is the breaking up of (typically) heavy nuclei to make lighter ones.

      e.g. U235 + n => Ba141 + Kr92 + 3n + energy

    • Stars are fueled by fusion
      • Not enough heavy elements

    Atomic
    Nuclei


    Stellar
    Cores

    • Tcore~15x106 K
    • Particles move very fast.
    • Collision results in:
      • Deuterium + Positron + Neutrino + Energy

    Reactions
    in Stars
    • Proton-Proton Chain
      • Most efficient in lower mass stars
      • T > 10,000,000 K
    • CNO Cycle
      • Most efficient in higher mass stars
      • T > 16,000,000 K
      • Hans Bethe (Cornell) 1939

    P-P chain:

    The P-P Chain: Reactions

    The P-P Chain: Illustration


    CNO cycle:

    The CNO Cycle: Reactions

    • Carbon is the catalyst for the reaction. It is returned to be used again!


    CNO cycle:

    The CNO Cycle: Illustration

     

    The
    Neutrino
    • A particle produced in stellar nuclear reactions is the neutrino, designed by the the Greek symbol n
    • The neutrino has no charge & small mass (close to zero)
      • - very little interaction with matter
    • The Sun is transparent to neutrinos.
    • "Neutrino telescopes" can look at the interior of the Sun.
    • Tank of chlorine (cleaning fluid) in S. D. mine. n's occasionally interact to convert Cl37 to Ar37
    • There appear to be too few n's!

    Energy
    Transport
    in Stars
    • How does the energy get out?
    • Energy can be transported by
      • Conduction
      • Convection
      • Radiation
    • Stars use the latter two methods
    • The trade between convection and radiation depends on the star and region within a star

    Model
    of the
    Sun

     

     

    Region
    Temp. (106 K)
    Density
    (g/cm3)
    Energy
    Transport
    Core
    15~
    100
    Convective
    Radiative zone
    3~
    1
    Radiative
    Convective zone
    1~
    0.1
    Convective

     

    Interiors of
    Stars


    Energy
    Transport
    Summary
    • Massive stars (> 2 Msun) have small convective cores and large radiative envelopes.
    • Low mass stars (< 1 Msun) have small radiative cores and large convective envelopes.


    Balance
    of
    Life
    • Hydrostatic Equilibrium is the balance of gravity and pressure in each layer of a star.
    • It keeps a star from collapsing (or expanding).
    • This balance is maintained as a star ages, so that its size might shrink or grow to maintain it.

     

    Lecture 17: Stellar Evolution

    Lecture
    Topics
    • The Interiors of Stars
    • How stars "evolve"
      • Main-sequence evolution
      • Giants and Supergiants
    • Nucleosynthesis
      • How are elements made?

    M-S
    Evolution
    • Fusion is occurring in the cores of stars
    • H is being converted into He
    • Since 4 particles are converted to 1, the pressure drops.
    • The core collapses and heats up.
    • This heats the outer layers which expand outward.

    Stars Evolve, even on the Main-Sequence


    The Sun
    on the
    M-S
    • 5 billion years ago:
      • Beginning of its life on main-sequence
      • Sun had 1/3 luminosity it has now.
    • 5 billion years from now:
      • End of its life on main-sequence
      • Sun will have twice the luminosity it has now.

    Stellar
    Evolution
    • When H is exhausted, the core shrinks.
    • It heats up but can not yet burn He, which needs 100,000,000 K!
    • The high temperatures ignites a shell of H around the core.
    • The increased pressure drives the envelope of the star outward.
    • Creating a giant or supergiant.


    Giant
    and
    Supergiant Stars
    • Expanded stars: very large radii
      • => large luminosity ( L = 4*pi*R2 sigma*T4 )
    • Uneasy stellar evolutionary stage
    • Variability
    • Mass loss
    • Very high temperature in the core

     

    Late
    Stages of
    Stars
    • The Helium Flash:
    • When Tcore ~ 108 K, He begins to burn.
      • He4 + He4 => Be8
      • He fusion in the core and H shell burning
    • Eventually He in core is exhausted
      • Contraction of the core raises the temperature further
      • Ignites He shell And have He and H shell burning.


    Evolution
    of the
    Sun

    Path in the H-R diagram of a 1 Msun Star


    Evolution
    of a Massive
    Star

    Path in the H-R diagram of a 20 Msun Star


    Time Scales
    of Stellar
    Evolution

    Mass (Msun)
    Formation (years)
    Main-seq (years)
    Giant Phase (years)
    1
    1x108
    9x109
    109
    5
    5x106
    6x107
    107
    10
    6x105
    1x107
    106

    Star
    Stuff
    • The conversion of H into He is not the only nuclear reaction that can take place in stars.
    • All elements other than H and He are produced from stars (or explosions of stars.)

    The material in you was formed by a star!

    The process of building up heavy elements from light ones is called nucleosynthesis.

    Nucleosynthesis
    • Formation of the elements.
    • "Heavy" elements can only be formed from H and He at very high temperatures and densities.
      • This can happen if the star is massive enough
    • The cores of giant and supergiant stars!!

    .
    .
    4 H1
    =>
    He4
    He4
    +
    He 4
    =>
    Be8
    Be8
    +
    He 4
    =>
    C12
    C12
    +
    He 4
    =>
    O16
    O16
    +
    He 4
    =>
    Ne20
    Ne20
    +
    He 4
    =>
    Mg24
    .
    .
    .
    .
    ...up to Fe56

     

    Energy
    Release

    Energy from Fusion and Fission

    Energy is released when elements lighter than iron are fused together. Likewise energy is released when element heavier than iron are split apart (fission). Conversely, to fuse heavier elements or split light elements requires extra energy.

    The plot below shows the "binding energy" per nucleon versus mass number. Iron is the most tightly bound nucleus. This means that moving towards iron releases energy. It is like a ball rolling to the lowest point.

    Binding energy of atomic nuclei

    Turning to
    Iron
    • The most stable element is Iron (26Fe56).
    • Need energy to split up Fe or to add to Fe.
    • For elements lighter than iron:
      • Fusion releases energy
    • For elements heavier than iron:
      • Fission releases energy
    • The universe is slowly turning to iron!

    The Core of an Evolved Star

    • An element factory!
    • An "onion skin" of different elements.
    • An iron core - if the star is massive enough.

    Most
    Common
    Elements

     

    Element
    Atomic Weight (amu)
    Relative Number
    H
    1
    1.0
    He
    4
    0.16
    O
    16
    9.0x10-4
    Ne
    20
    5x10-4
    C
    12
    4x10-4
    N
    14
    1.1x10-4
    Si
    28
    3.2x10-5
    Mg
    24
    2.5x10-5
    Fe
    56
    4.0x10-6
    Ni
    59
    1.0x10-6
    ...
    >60
    1.0x10-7

     

    Abundances
    of Chemical
    Elements


    Life Cycle
    of Stars
    • Birth:
      • Gravitational Collapse of Interstellar Clouds
      • "Hayashi Contraction" of Protostar
    • Life:
      • Stability on Main-Sequence
      • Long life - energy from nuclear reactions in the core (E = mc2)
    • Death: Lack of fuel, instability, variability
      • expansion (giants, supergiants),
      • explosions!!

     

    Lecture 18: Neutron Stars and Pulsars

    Lecture
    Topics
    • Neutron Stars
    • Pulsars

    Neutron
    Star
    • An extremely dense sea of neutrons.
    • A giant atomic nucleus in the sky!!
    • Mass = 1.4 to ~3 Msun
    • Size ~ 10 km
    • Density ~ 3 x 1014 g/cm3
    • Intense magnetic fields, rapidly rotating.

    Neutron
    Star
    Density
    • Neutron Star density ~ 3 x 1014 g/cm3
    • Steel has a density of 7.7 g/cm3

    The mass of a 1 cm cube of a Neutron Star is equivalent the mass in a 340 meter cube of steel!


    Neutron
    Star
    Rotation
    • Neutron stars initially spin very rapidly.
    • Conservation of angular momentum!
      • mass x velocity x radius = constant
    • Rotation period of Sun = 25 days
    • Shrinking the Sun to 10 km would give
      a rotation period of much less than 1 second!

    The Discovery
    of Pulsars
    • Jocelyn Bell - 1967
      • Graduate student at Cambridge, England
      • Discovered a pulsating radio signal coming from the sky!!
    • LGMs? (Little Green Men)
    • The object is a pulsar (pulsating star).
    • Antony Hewish (her advisor) won a Nobel Prize.

    Pulses
    from
    Space
      A short pulse is detected at regular intervals.

    Pulsars
    are
    Rotating Neutron
    Stars
    • Rotation Periods ~ 0.001 to 10 seconds.
    • Pulsars cannot be normal stars!
    • Even a white dwarf would fly apart!
    • T. Gold (Cornell) and F. Pacini (Italy) made the connection between pulsars and neutron stars.
    • Magnetic Field ~ 1012 gauss.

    Lighthouse
    Theory of
    Pulsars
    • The intense magnetic field rips particles from the surface at the magnetic poles.
    • As the particles are accelerated to relativistic speeds, the electrons emit synchotron radiation.
    • The radiation is highly directional and photons are concentrated in narrow beam coming from the polar cap.
    • The magnetic pole is not aligned with the rotation axis (like the earth).
    • So the beam of radiation sweeps around the sky.
    • We see a pulse when the beam points towards us.
    • Pulsars slow down because they are radiating energy away!

    Pulsar
    "Discoveries"
    • Pulsars are excellent clocks!
    • Binary Pulsar (General Relativity test)
      • Slow down of orbit confirms General Relativity.
      • Won Nobel Prize for Taylor and Hulse
      • Work done at Arecibo Observatory
    • Pulsar in an Eclipsing Binary
    • Planets around Pulsars!

    Pulsar in
    and Eclipsing
    Binary

    • Pulsar period = 0.0016 seconds!
    • Pulsar orbits companion every 9.7 hrs.
    • Pulsar is eclipsed for 50 minutes each orbit.
    • Masses: Pulsar ~ 1.4 Msun
      • Companion ~ 0.023 Msun
    • The pulsar may be evaporating the companion.
    • In about a billion years it may be gone.

    Planets
    Around
    Pulsars
    • Accurate timings of radio pulses from Pulsar PSR 1257+12 show evidence for small bodies orbiting it.
    • This pulsar is ~300 pc (~980 lightyears) away.
    • Three planet size objects have been detected!

    Planet

    Mass
    (Mearth)

    Distance from Star
    (AU)

    Orbital Period
    (days)

    A

    0.015

    0.19

    25.34

    B

    3.4

    0.36

    66.54

    C

    2.8

    0.47

    98.22


    PSR 1620-26
    • It is thought that a planet has been detected orbiting Pulsar PSR 1620-26, which is about 3.8 kpc (12400 lightyears) from us.

    Planet

    Mass
    (Mjupiter)

    Distance from Star
    (AU)

    Orbital Period
    (years)

    -

    < 10

    ~ 20

    ~ 100


    X-Ray
    Binaries
    • Mass falling from companion on the NS emits x-rays
      • The falling material reaches such high speeds, when it hits the stars the temperature becomes very high
      • Hence, emission is in the x-ray part of the spectrum.

    Lecture 19: The Milky Way and Other Galaxies

    Lecture
    Topics
    • The Milky Way
      • Molecular Gas
      • The Galactic Center
      • Mass of the Galaxy
      • The Star-Gas-Star Cycle
    • Discovering galaxies
      • The "great" debate
      • Hubble's discovery
    • Types of galaxies

    Molecular
    Gas
    • Molecular "Ring"
      • from 4-8 kpc and concentration on GC
      • Thickness ~ 120 pc.
    • Giant Molecular Clouds (GMCs):
      • Size ~ 10 - 50 pc, Mass ~ 103 - 106 Msun
      • Stars form in cores of GMCs.
    • Mass ~ 3 x 109 Msun, ~2/3 inside the orbit of the Sun around the Galactic Center.

    The Molecular
    Gas Distribution



    The Galactic
    Center
    • What lies at the center of our Galaxy?
      • Dust obscures the visible light from us
      • Use radio and infrared observations
    • Dense star cluster peaks at the center.
      • ~ 2 x 106 Msun within 1 pc
      • Stars only 1000 AU apart
      • A collision every 106 years!
      • Bright radio source. (black hole?)
    • A massive "molecular ring" of gas and dust rotates around this star cluster
      • Extends from ~ 1 to 5 pc from the center
      • "Leaking" matter into the center
    • Structures outside the molecular ring
      • 20 pc long linear structures tracing Galactic magnetic fields
      • isolated star forming regions

    Star-Gas-Star
    Cycle
    • The ISM provides the matter from which stars form.
    • Stars evolve and create "heavy" elements
      • Through stellar nucleosynthesis and supernovae
    • These elements are returned to the ISM.
      • Stellar winds, planetary nebula, and supernovae
      • Not all material is returned resulting in the gas being “used up”
    • The “enriched” gas is used by the next generation of stars.

    Galaxy
    Rotation
    • The stars and gas rotate about the center of the Galaxy.
    • The rotation speed varies with distance from the center.
    • From the speed at a given point, we can deduce the mass.

    Kepler's Law
    for the
    Galaxy
    • The total mass of the galaxy can be computed from Newton's laws
      • Like the mass of binary stars
    • From Lecture 16 (Binary Stars), we have Newton's version of Kepler's third law

    Kepler
    Modified by
    Newton
    • For a circular orbit

    • Combining this with Newton's version of Kepler's third law gives.


    Example
    Rotation
    Curves
    • A rotation curve represents the velocity of particles versus distance from the center of rotation.
    • Two examples are:
    • Merry-go-round - the velocity increases (linearly) with increasing distance. This is also called "solid body rotation". This is shown below.

    • Solar system - the velocity decreases (as 1/square-root(r)) with increasing distance. The rotation curve follows Kepler's law, as shown below.

    Figures from "The Cosmic Perspective" by Bennett et al.


    Galaxy
    Rotation
    Curve
    • The rotation curve for the Milky Way is relatively flat.
    • It is more like the merry-go-round than that of the solar system
      • Thus there is no dominant central mass

    Figure from "The Cosmic Perspective" by Bennett et al..


    Mass of the
    Galaxy
    • Using Newton's form of Kepler's third law we can deduce the mass of the Milky Way at different distances from the center.
    • For the Sun, v = 220 km/sec at a radius of 8.5 kpc.
      • Orbital period = 240 million years.
    • Mass of MW = 1011 Msun within 8.5 kpc.

    Dark
    Matter
    • The mass seen in stars is much less than that derived from Newton's laws.
    • Conclusion: there must be some additional mass which is non-luminous!
    • The is unseen mass is call Dark Matter.
    • It is called missing mass because starlight cannot trace it.

    Formation of
    the
    Galaxy
    • The Galaxy collapsed from a cloud of gas and dust due to its own self-gravity.
    • Some (Pop II) stars formed first.
    • Remaining gas collapses into a disk - angular momentum conservation!
    • First generation massive stars eject metals into the disk so that
      • Pop I stars have higher metallicities

    The Curtis-Shapley
    Debate
    • April 26, 1920
    • Debate on "The nature of spiral nebulae" & "The size of our galaxy"
    • Heber Curtis vs. Harlow Shapley
    • Shapley claimed spiral nebulae were "close"!!

    Edwin Hubble
    • Discovered Cepheid variables in M31 (Andromeda Galaxy)
    • Used the Period-Luminosity Relation for Cepheids
    • Determined that M31 is a galaxy, an "Island Universe"

    Periodic Variable
    Stars
    • A small fraction of stars have brightness variations that are periodic.
      • Due to "radial oscillations" (pulsations which cause expansion and contraction)
    • These are stars which have evolved off the main-sequence (post main-sequence stars).
    • Two types:
      • RR Lyrae Variables
      • Cepheid Variables
    • Although the periods from 0.5 to 100 days, any given star has a constant period.


    RR Lyrae
    Variables
    • Horizontal branch stars (because of where they appear in the H-R diagram).
    • Periods: ~ 12 to 24 hours
    • Luminosity: ~ 50 Lsun
    • Found in Globular clusters (Pop II stars)
    • Luminosity is independent of period

    Cepheid
    Variables
    • Named after delta Cephei (first discovered) Red Giants and Supergiants
    • Periods: ~ 1 to 100 days
    • Luminosity is a function of period
      • Period-Luminosity relation discovered by Henrietta Leavitt in 1908.
    • There are two types (labelled Type I and II Cepheids)

    Type I
    Cepheids
    • a.k.a. Classical Cepheids
    • Luminosity: 400 to 20,000 Lsun
    • Location: Open clusters and the galactic disk (Pop I stars)

    Type II
    Cepheids
    • a.k.a. W Virginis Stars
    • Luminosity: 100 to 5,000 Lsun
    • Location: Globular clusters (Pop II stars)

    Period-Luminosity
    Relation`



    Distances with
    P-L Relation
    • Measured Period gives:
      • Luminosity
      • Mv (absolute magnitude)
    • Measure mv (apparent magnitude)
    • Mv and mv => distance from distance modulus equation
      • mv - Mv = - 5 + 5 log10 (d)
    • A Hubble "key project" is to determine the distances to galaxies w/ Cepheids.

     

    Lecture 20: Normal and Active Galaxies

    Lecture
    Topics
    • Galaxy Properties
      • Classifying galaxies
    • Local Group
    • Clusters of galaxies
    • Active galaxies
    • What powers these things?

    Galaxies
    • A galaxy is a collection of stars, gas and dust along w/ associated starlight, magnetic fields and cosmic rays.
    • Four broad categories:
      • E: elliptical
      • S: spiral (normal & barred)
      • S0: lenticular
      • I: irregular

     

    Elliptical
    Galaxies
    • Range from spherical to highly flattened
      • with designations E0 to E7
    • Contain old stars (Pop II)
    • Very little gas and dust
    • 1-200 kpc in diameter
    • Mostly found in clusters of galaxies
    • Average spectral type: K
    • 106 to 1013 Msun

    Spiral
    Galaxies
    • Flattened systems which have a thin disk
    • Display spiral structure.
    • Divided into barred (SB) and unbarred (S) spirals.
    • Further subdivided into classes a, b, and c; e.g. SBb, Sc, ... where:
      • a => large nuclear bulge & tightly wound spiral arms
      • c => small nuclear bulge & loosely wound spiral arms
    • Contain young (Pop I) and old (Pop II) stars
    • Copious amounts of gas and dust
    • 5-50 kpc in diameter
    • Found mostly in the "field" (outside clusters)
    • Average spectral type: A, F, G, K
    • 109 to 1011 Msun

    Lenticulars
    • Similar to spiral galaxies in shape and color but no spiral arms
    • Flattened systems which are morphologically between ellipticals and spirals.

    Irregulars
    • By definition, irregular in shape
    • Mostly young stars (Pop I)
    • Lots of gas and dust
    • 1-10 kpc in diameter
    • Found in the field (outside clusters)
    • Average spectral type: A, F
    • 108 to 1010 Msun

    Hubble
    Tuning
    Fork Diagram



    • The classification scheme is strictly morphological (based upon physical appearance) and does not necessarily imply an evolutionary sequence.
    • The morphological transition is smooth, but a galaxy may stay the same type for its entire lifetime.

    Other types
    of Galaxies
    • Dwarfs
      • 106 to 108 stars
    • Peculiar
      • Exploding, Ring, Disrupted
    • Seyfert
      • Very Bright Nucleus
    • N
      • Extremely Bright Nucleus
    • Interacting
      • Tidal Effects, Tails (pairs)
    • QSO
      • Collapsed Nuclei?

    "Nearby"
    Galaxies
    • LMC, SMC:
      • D ~ 50 kpc
    • M31 (Andromeda):
      • D ~ 700 kpc
    • Virgo Cluster:
      • D ~ 20,000 kpc = 20 Mpc

    The Local
    Group



    Galaxy
    Statistics
    • ~1/3 of all spirals are barred spirals.
    • There are "Field" and "Cluster" galaxies.
    • Ellipticals are most common in clusters.
    • Spirals are most common in the "field."

    Clusters of
    Galaxies
    • The Local Group is just outside the Virgo Cluster
    • Poor clusters have ~ 10 galaxies
    • Rich clusters have ~10,000 galaxies
    • Size of rich clusters: ~10 Mpc
    • Millions of clusters in the universe

    Superclusters
    • Clusters of clusters
    • The Local Group is part of the Virgo Supercluster
    • Large scale structures containing many clusters have been found.
    • Does clustering continue forever in the universe?


    Links to
    Galaxy
    Images


    M100 from HST (76K) M31 (NGC 224) (279K)
    Cepheids in M100 (56K) Whirlpool (NGC 5194) (160K)
    Cepheid pulsation in M100 (84K) NGC 598 (Sc in Tri) .
    Cepheid pulsation in M100 (84K) NGC 598 (Sc in Tri) .
    NGC 205 (Satellite of Andromeda) (136K) M33 (NGC 598) (91K)
    M87 (30K) LMC .
    NGC 4594 (Sab in Virgo) (136K) Leo I Dwarf Sph. .
    NGC 3031 (Sb in UMa) (188K) NGC 6822 .
    NGC 253 . Centaurus A .
    NGC 2997 . Cen A (longer exp.) .
    NGC 1566 (Seyfert) . Virgo Cluster .
    M83 (39K) . . .

     

    Active
    Galaxies


    Galaxy

    Luminosity (LMW*)

    Normal

    < 10

    Seyfert

    0.5 - 50

    Radio

    0.5 - 50

    Quasar

    100 - 5,000

    * where LMW = Luminosity of Milky Way = 2x1010 Lsun

     

    Seyfert
    Galaxies
    • Spectral lines don't resemble normal stars.
      • Highly ionized heavy elements, e.g. iron!
      • Lines very "wide" => tremendously hot (>108 K) or rapidly rotating (~1000 km/s)
    • Nearly all emission comes from the galactic nucleus (a small central region).
      • ~ 104 times brighter than the center of our galaxy
    • Most energy emitted in infrared and radio parts of the spectrum.
      • Look very much the same as normal galaxies in the visual.
    • Emitted energy varies with time!
      • => Compact source of energy
      • => Emitting region < 1 lyr across
      • Some emit more light than the Milky Way!

    Radio
    Galaxies
    • Very bright in the radio
      • Cosmic rock stations?
    • Core-Halo radio galaxies
      • Most emission from a very small core
        (< 1 parsec across)
    • Extended (or Lobe) radio galaxies
      • Emissions extend hundreds of kiloparsecs!

    Core-Halo
    Radio
    Galaxies


    Extended
    Radio
    Galaxies



    Links to
    Radio
    Galaxies
    • Cygnus A
    • Cygnus A close-up
    • Hercules A
    • 3C75, Multi-Jets
    • Jet in NGC 6251
    • Jet in M87

    These links are not yet enable. You'll find images some images at the Space Telescope Science Institute - Interesting Astronomy links page.


    Quasi-Stellar
    Objects (QSOs)
    • Galaxies with extremely luminous sources
      • Look like stars in photographs.
      • Some evidence of faint "parent" galaxy
    • Energy originates in a very small region.
    • QSOs are variable
    • Can see to great distances
      • Most distant objects seen in the universe
    • Such a source at 50 pc would appear as bright as the Sun!

     

    • Quasar: quasi-stellar radio source
      • a subset which is a strong radio emitter

    What Powers
    These?
    • We need to produce up to 5,000 times the luminosity of the Milky Way yet within a region ~1 pc in size !!!!
    • Leading theory is a black hole with an accretion disk:
      • Material gains energy as it falls towards the black hole.
      • The gas heats up, and radiates energy.

    Accretion Disk
    Model



    Energetics
    • Material needs to keep flowing onto the black hole to power the source.
    • 1 Msun / decade => ~ 10 LMW
    • 10,000 LMW => 100 Msun / year!!
    • Large black holes (108 - 109 Msun) are needed to fit the models, otherwise the accretion disks blow themselves apart.