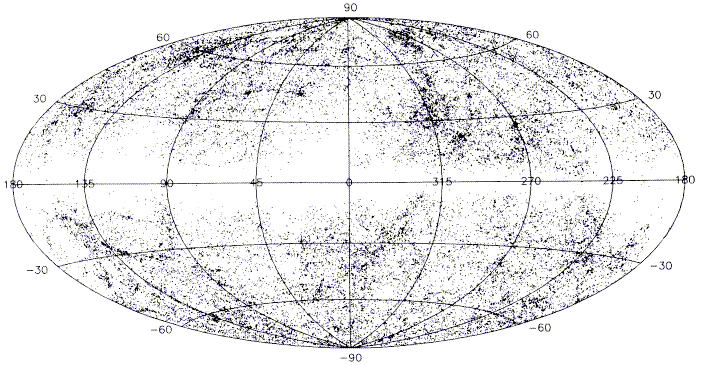
The earliest studies (back to the Messier catalog, had anyone known what all those blobs in the spring sky meant) showed that clumps of galaxies exist - such as the prominent ones in Virgo and Coma. It was long held that only a small fraction of galaxies were involved, so that clusters would be rare collections superimposed on a smooth "field". All-sky surveys (such as those from large Schmidt telescopes) changed this view. The distribution of galaxies to a given magnitude shows considerable structure, as shown in this map from Sharp 1986 (PASP 98, 740, from the ADS) for galaxies to B=14.5 (merging the UGC, ESO, and MCG catalogs):

Abell (1958, ApJSuppl 3, 211) identified 2712 rich clusters on the Palomar survey plates, producing the basic sample for later statistical studies. Abell based his rough classifications on the number of cluster members within an Abell radius (which scales with the expected cluster redshift, more or less 1 Mpc) and the number of members within 3 magnitudes of the brightest galaxy, assigning richness and distance classes to each cluster. Zwicky and coworkers (Catalog of Galaxies and Clusters of Galaxies = CGCG, vols. 1-6, 1961-68) found many looser clusters. The Abell clusters have been tabulated with up-to-date information by Struble and Rood 1987 (ApJSuppl 63, 543 and 555). The survey of clusters was extended to the southern sky by Abell, Corwin, and Olowin 1989 (ApJSuppl 70, 1; CDS digital version), producing the first reasonably complete all-sky catalog of nearby clusters (some as far away as z=0.4). The Abell survey was remarkably reliable, with only about 10% of the clusters at z < 0.1 being fakes produced by superpositions of sparser groupings (Katgert et al. 1996 A&A 310, 8).
Clusters have a wide range of richness, size, and internal structure in the distribution of galaxies. It is hard to draw a line between groups and clusters. We are located in a rather distinct subgroup on the outskirts of the Virgo Cluster, viz. the Local Group. It is now recognized to contain the following members; possibly bound satellites of the Milky Way and Andromeda are placed with their putative central galaxies. The edges of the Local Group are not as well-defined as one might like; not only distance but kinematics enter, through the zero-velocity surface at which the Hubble expansion would overcome the binding potential of the group. An up-to-date list of members is maintained by Mike Irwin. My tabulation follows Courteau and van den Bergh (1999 AJ 118, 337) and adding Cetus from Whiting, Hau, and Irwin (1999 AJ 118, 2767).
| Galaxy | Type | MB | RA/Dec | l, b | D (kpc) | vr (km/s) |
| Milky Way | Sbc I-II | -20.0 | 1830-30 | 0 0 | 8.5 | 0 |
| LMC | SBm | -18.4 | 0524-60 | 280 -33 | 50 | 270 |
| SMC | Im | -17.0 | 0051-73 | 303 -44 | 63 | 163 |
| Sgr I | dSph? | -14.0 | 1856-30 | 6 -14 | 20 | 140 |
| Fornax | dE0 | -12.0 | 0237-34 | 237 -65 | 138 | 55 |
| Sculptor dE | E? | -10.6 | 0057-33 | 286 -84 | 80 | 110 |
| Leo I | dE3 | -9.6 | 1005+12 | 226 +49 | 220 | 168 |
| Leo II | dE0 | -8.5 | 1110+22 | 220 +67 | 220 | 90 |
| Ursa Minor | dE4 | -8.2 | 1508+67 | 105 +45 | 63 | -209 |
| Draco | dE0 | -8.0 | 1719+58 | 86 +35 | 75 | -281 |
| Carina | dE | -8.5 | 0640-50 | 260 -22 | 91 | 229 |
| Sextans | dSph | -9.4 | 1010-01 | 243 +42 | 85 | +230 |
| M31 | Sb I-II | -21.6 | 0040+41 | 121 -22 | 730 | -297 |
| M32=NGC 221 | E2 | -15.5 | 0039+40 | 121 -22 | 730 | -200 |
| NGC 205 | E5p | -15.7 | 0037+41 | 121 -21 | 730 | -239 |
| NGC 185 | E3P | -14.6 | 0036+48 | 121 -14 | 730 | -202 |
| NGC 147 | E5 | -14.4 | 0030+48 | 120 -14 | 730 | -193 |
| And I | dE3 | -10.6 | 0043+37 | 122 -25 | 730 | --- |
| And II | dE | -10.6 | 0113+33 | 129 -29 | 730 | --- |
| And III | dE | -10.6 | 0032+36 | 119 -26 | 730 | --- |
| Cas=And VII | dSph | 2326+50 | 109 -09 | 690 | --- | |
| Pegasus=DDO 216 | Ir V | -12.3 | 2328+14 | 94 -43 | 760 | --- |
| Peg II=And VI | dSph | -10.6 | 2351+24 | 106 -36 | 830 | --- |
| LGS 3 | dIm | -10.3 | 0101+21 | 126 -41 | 800 | -277 |
| M33 | Sc II-III | -19.1 | 0131+30 | 134 -31 | 900 | -179 |
| NGC 6822 | Im | -15.3 | 1942-15 | 025 -18 | 680 | -57 |
| IC 1613 | Im | -14.8 | 0102+01 | 130 -60 | 850 | -234 |
| Sgr dI | Im | -10.5 | 1927-17 | 21 +16 | 1100 | -79 |
| WLM | IBm | -14.0 | 2359-15 | 76 -74 | 860 | -116 |
| IC 10 | Im | -16.2 | 0017+59 | 119 -03 | 1200 | -344 |
| DDO 210, Aqr | Im V | -10.8 | 2044-13 | 34 -31 | 1000 | -137 |
| Phoenix | dIm | -8.8 | 0149-44 | 272 -68 | 450 | +56 |
| Tucana | dSph | -8.8 | 2241-64 | 323 -48 | 870 | --- |
| Leo A=DDO 69 | Ir V | -11.5 | 0959+30 | 196 52 | 690 | --- |
| Cetus | dSph | -10.1 | 0026-11 | 101 -72 | 770 | --- |
A few other galaxies (GR 8, IC 5152, at 1.5 Mpc or so) may or may not dynamical members of the Local Group. The number of dwarfs close to the Milky Way, the fact that the distant dwarfs are more luminous on average, and the number of members found since the last time I updated this table, all suggest depressing things about how incomplete our surveys may be even around M31. van den Bergh (1992 A&A 264, 75) fits a Schechter form to the luminosity function of Local Group members and finds MB* =-22.5 and a faint-end asymptotic slope a=-1.1, still not as steep as some field surveys but sampled much fainter. The Local Group is still a dynamically active environment, if we may judge from tidal stripping of M32, the imminent demise of the newly-found Sagittarius dwarf spheroidal from galactic tides, and the material pulled into the Magellanic Stream for the same reason.
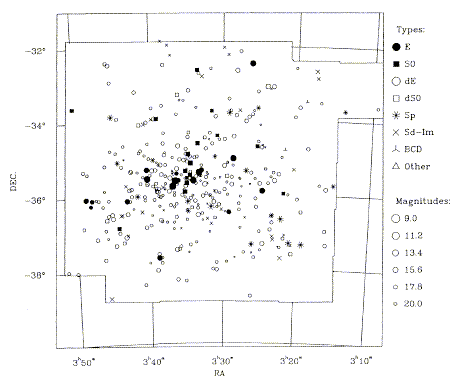
Numerous similar groups exist nearby - Sculptor, M81, the M101 or CVn cloud, etc. In Virgo we find a much richer aggregation, at the cluster core. Here are giant ellipticals (with M87 at the center being a D galaxy), spirals of all types, dwarfs, etc., making this a crucial environment for calibrating distace indicators. A few times farther away, we find the Hydra I and Centaurus clusters (not to be confused with the Cen A group), beyond which things get populous as more volume is sampled. Coma (about 5 times the Virgo distance) is the nearest rich, regular cluster and a useful standard of comparison. Even some ``small groups" contain of order 100 members when surveyed to faint levels, as seen in the map of the Fornax group from Ferguson and Sandage (AJ 100, 1, courtesy of the AAS):
Groups may be picked out (with redshift data) in several ways. Local density contrast and "friends-of-friends" techniques are popular, remembering that velocities don't tell much about distance within a group since group velocity dispersions are comparable to the internal velocities in luminous galaxies (~ 300 km/s). Numerous papers have catalogued groups in various ways; the main point may be that most galaxies can be plausibly assigned to groups at the scale of ours or more numerous.
Compact groups pose some special puzzles. As listed, for example, by Hickson (1982 ApJ 255, 382), they consist of 4-7 galaxies within an area of only a few hundred kpc diameter. They contain more spirals than expected from the usual morphology-density relation, and have very short predicted lifetimes against merging. Furthermore, the number of position-selected members with discordant redshifts is rather high (~1/3); this makes Stephan's Quintet (below) a very good prototype of all the issues involved. Various workers have considered them to be real but young, the dregs of a once-rich population, constantly forming from more diffuse group environments, long filaments seen lengthwise, and fictitious chance alignments. Recent work on Stephan's Quintet has muddied the waters further, implying a crucial role for bound or captured high-velocity members in pumping the group's energy and keeping it from merging. See the WFPC2 images of Stephan's Quintet, Seyfert's Sextet or NGC 6027, and HCG 87 to watch some of these interactions at work.

Genuine clusters exhibit a wide range of galaxy population and content, and are luminous enough to be sampled across large distances. I'll stress at the outset that the visible galaxies are such a minor part of the whole assemblages, and are probably even outweighed by the hot intracluster gas, that "cluster of galaxies" is downright misleading, but we're stuck with it. To make matters worse, I've split off treatment of the gas to a separate section, and the treatment of the galaxy content of clusters and its evolution to the "environmental impact" section.
Some order has been brought to cluster study by several classification schemes (see review by N. Bahcall 1977 (ARA&A 15, 505). These may be based on:
Schemes based on these correlate reasonably well with one another. Zwicky distinguished compact, medium-compact, and open clusters, with or without strong central concentrations. The Rood and Sastry (RS) classification is based on the projected distribution of the brightest 10 members (being appropriately cautious about possible interlopers). They recognize these types:
| cD - single dominant cD galaxy (A2029, A2199) | C - single core of galaxies |
| B - dominant binary, like Coma | F - flattened (IRAS 09104+4109) |
| L - linear array of galaxies (Perseus) | I - irregular distribution (Hercules) |
These appear to have affinities in a tuning-fork pattern:
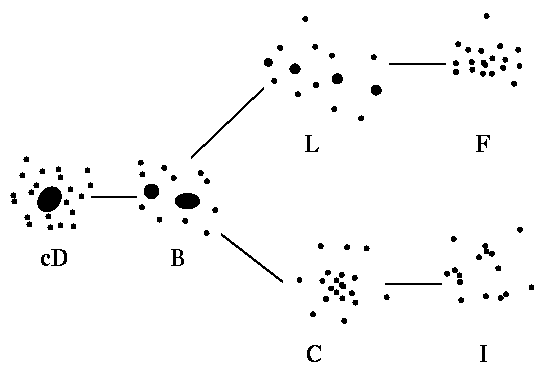
with concentration generally increasing leftward. However, some poor clusters do have cD galaxies, perhaps the result of runaway merging.
The Bautz-Morgan classification is based on brightness contrast between first- and second-ranked galaxies (i.e. the slope of the luminosity function at the bright end):
| I | central cD galaxy (A2199) |
| II | intermediate E/cD (Coma) |
| III | no dominant galaxy (Virgo, Hercules) |
Intermediate stages I-II,II-II are recognized.
The classifications compare roughly as follows, based on an early Annual Reviews article:
| Property/Class | Regular (Early) | Intermediate | Irregular (Late) |
| Zwicky type | Compact | Medium-Compact | Open |
| Bautz-Morgan type | I, I-II, II | (II), II-III | (II-III), III |
| Rood-Sastry type | cD,B, (L,C) | (L),(F),(C) | (F), I |
| Content | Elliptical-rich | Spiral-poor | Spiral-rich |
| E:S0:S ratio | 3:4:2 | 1:4:2 | 1:2:3 |
| Symmetry | Spherical | Intermediate | Irregular shape |
| Central concentration | High | Moderate | Very little |
| Central profile | Steep | Intermediate | Flat |
| Mass segregation? | Marginal | Marginal | None |
| Radio emission? | 50% | 50% | 20% |
| X-ray luminosity | High | Intermediate | Low |
| Examples | A2199, Coma | A194,A539 | Virgo, A1228 |
Is the implied sequence one of total mass, mass concentration, or status of dynamical evolution? These are probably correlated too. Some additional properties of clusters vary with concentration (or extent of relaxation or richness, all of which are related). These include:
Galaxy content: the fraction of E/S0 galaxies depends on local galaxy density (Dressler 1980 ApJ 236, 351) and thus changes markedly from the outskirts to a cluster core (see the environmental-impact lecture. Only loose or subcluster environments have many spirals. As we've already seen, this changes with cosmic epoch in the Butcher-Oemler effect.
Symmetry: the most concentrated clusters are most symmetric and regular, approaching in some cases an equipartition distribution. One may seek substructure in position or velocity space.
Mass segregation: If the cluster evolves far enough dynamically, energy will be equally distributed among members, so that the more massive ones move more slowly and sink to the center. There is some evidence for this effect in a few clusters.
Velocity dispersion: this is a total-mass indicator, and is generally largest for rich, regular, relaxed clusters. An unbiased (or maybe only slightly biased) virial mass estimator is given by Heisler et al 1985 (ApJ 298, 8) as
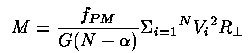
where Vi is the radial velocity of galaxy i with respect to the cluster mean, R ^ is the projected distance from the cluster center, a~1.5 is a fudge factor accounting for the fact the the center must be determined from the galaxy positions themselves, and fPM depends on the typical orbital shape; it has values 32/p for isotropically distributed orbits and 64/p for purely radial orbits. See also the discussion of mass estimators by Postman, Huchram and Geller 1988 (AJ 95, 267).
One might well ask whether and how clusters blend into groups and any larger structure. Peebles championed the use of a correlation function as a statistical probe for this (see his book Large-Scale Structure of the Universe, Princeton 1980). The correlation function x measures the association of galaxies on some linear scale R such that for uncorrelated positions x=0. By definition, the probability distribution of other galaxies with distance R from a given galaxy is
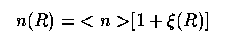
which has the observed form from catalog data
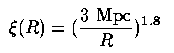
This can be directly measured, since the correlation function projected onto two dimensions can be shown to have a slope flatter by exactly unity than the three-dimensional function. Higher-order correlation functions (three-point, four-point, etc.) may be defined, but tend to get lost in the noise. This statistic is very robust, but loses much of the total information content of clustering. Its value lies in pulling together pairs, groups, clusters, and larger-scale structures into a single unbroken statistical description of the galaxy distribution. If we know how light traces mass, this can be transformed into the power spectrum P(k) which tells how the clustering power (amplitude of the density field) is distributed with wavenember k, which is a prime prediction of various theories for the production of structure in the early Universe. The power spectrum is related to the full set of (mass) correlation functions through a Fourier transform.
There are other clustering descriptors, such as percolation analysis or "friends-of-friends". In this approach, one asks what fraction of galaxies in a sample are connected to neighbors within a given distance as this distance is changed.Last changes: 2/2003 © 2000-3