

Next: Chemical evolution models
Up: AY616 class notes
Previous: Observable global properties of
- Both luminosity and spectrum depends on stellar content of the galaxy, and
understanding these is the subject of stellar populations.
- Use stellar evolution theory to interpret differences in stellar pops
between galaxies
- consider the spectrum of a galaxy to be the sum of a set of
simple stellar populations (SSPs)
- SSPs are single-age, single-metallicity population.
- Spectrum of a SSP depends three quantities: the age, metallicity and
IMF, plus an understanding of stellar evolution and atmospheres.
- try to determine the relative amplitudes of all possible
SSPs in a given galaxy spectrum, and hence get the star formation
history. Note that SFH is combination of age distribution, metallicity
distribution, and initial mass function (time dependent?)
- quick review of stellar evolution
- Stellar evolution gives model tracks
(evolution as function
of time for a given mass)
- MS, SGB, RGB (note relative constancy of tip luminosity with stellar
mass), HB, AGB, PAGB, WD (or SN), advanced stages for
higher mass stars.
- What is going on inside the star at each stage? Hydrogen
and helium burning sequences: HB morphology, red clump stars,
blue loop stars.
- cross section of properties at fixed time across a range of
masses is an
isochrone (e.g., Renzini fig 1.6)).
- Age effects (show model isochrones)
- Metallicity effects: atmosphere effects and internal effects.
Observed metallicity effects: RGB, HB morphology.
(show model isochrones)
- Other effects? Second-parameter problem (show second parameter
data). Extreme HB stars.
Age? He abundance? Heavy element abundances? Density? Rotation?
- Potential importance of binaries/interactions: SNIa and
blue-stragglers.
- Integrated luminosity of a population
- since post-MS evolution is fast compared to MS evolution
for all masses, it is true that at any given time when the most
luminous stars are the most evolved stars the luminosity is given
predominantly by stars of (nearly) a single mass. (true for
all except youngest ages, see Renzini 1.1),
- Do SSPs get brighter or fainter as they age?
- To determine the luminosity of a stellar population, consider the
number of stars evolving off the MS, or equivalently, dying,
which is given by the evolutionary flux:
measured in number
of stars per year, where 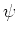 is the IMF, and
is the IMF, and 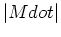 is the time
derivative of the turnoff mass.
( Renzini 1.1).
is the time
derivative of the turnoff mass.
( Renzini 1.1).
- one can see that the IMF is critical in determining the luminosity
evolution of a galaxy.
- Once one reaches an age where most massive stars have died, all
stars of lower mass reach comparable luminosity (tip of RGB),
hence luminosity of population depends on number of red giants
- For typical IMF, number of stars increases slower towards lower
mass than rate of generation of turnoff stars decreases
- Integrated mass of a population
- Mass contribution depends on IMF
- ``classical'' Salpeter IMF (power law with
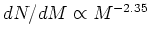 ) and
others (Pagel Fig 3).
) and
others (Pagel Fig 3).
- Widely used determination of local IMF is by Kroupa,
Tout, and Gilmore, who find
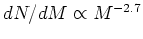 for
for 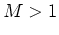 Msun,
Msun,
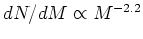 for
for 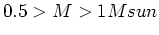 ,
,
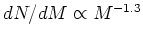 for
for 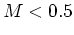 Msun.
For our purposes we'll assume that
Msun.
For our purposes we'll assume that 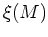 is normalized
to unit mass, i.e.,
is normalized
to unit mass, i.e.,
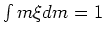 .
.
- For all measured IMFs, bulk of the mass is in relatively
low mass stars (
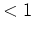 Msun).
Msun).
- Empirically, no strong evidence for variations of IMF as
functions of, e.g., metallicity.
- No well-established theory for predicting IMF
- Since most of integrated mass is in low mass, unevolved, faint, stars,
while most of luminosity comes from the more massive, brighter stars,
stellar populations can be parameterized in terms of stellar
mass-to-light ratio
- definition in terms of solar mass-to-light ratio.
- Absolute value of M/L depends strongly on IMF; relative
values characterize different stellar pops for fixed IMF.
- Typical synthetic M/L ratios for individual stars:
| Mass |
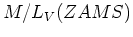 |
| 0.3 |
27 |
| 0.5 |
14 |
| 1.0 |
1.57 |
| 2.0 |
0.12 |
| 4.0 |
0.012 |
- M/L for simple stellar populations (solar metallicity and KTG IMF)
| Population age (Gyr) |
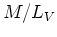 |
| 0.1 |
0.14 |
| 1 |
0.5 |
| 2 |
0.8 |
| 3 |
1.1 |
| 5 |
1.5 |
| 10 |
2.3 |
| 15 |
3.0 |
- M/L composite populations with constant SFR (solar
metallicity and KTG IMF):
| Population age range |
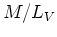 |
| 0.1-10 |
1.5 |
| 0.1-15 |
2.0 |
- stellar M/L ratio depends on luminosity bandpass; less variation as one
goes to near-IR bandpasses
- Note: people also talk about total mass to light ratios, i.e.,
including dark matter
- Integrated spectrum of a population
- need to know the relative contributions of each stage of evolution
- number of stars in each
post-MS stage is determined by the time spent in each stage:
and although the flux is sensitive to the IMF, the relative contributions
of each stage are not, at least for older populations
(Renzini fig 1.5).
- For all except the youngest population, the later stages of
stellar evolution provide a majority of the light.
- Consequently, many properties are
nearly independent of the IMF, including the integrated spectrum and
the relative contributions of various evolutionary stages.
- Integrated spectra can be predicted from stellar evolutionary models
- Potential problems with synthetic integrated spectra:
- stellar isochrone uncertainties, due to opacities, convection,
diffusion, mass loss, atmospheres, etc.; tend to be larger at
later stages of evolution (luminous stages!)
- missing evolutionary stages (e.g. HB, AGB, PAGB)
- missing components in models, e.g., SMR stars
- solar element abundance distribution
- interacting binary stars
- Some existing evolutionary synthesis compilations/codes:
- Bruzual & Charlot (e.g. MNRAS 344, 1000 (2003))
- Worthey ApJS 95, 107, 1994
- Bertelli et al., A&AS 106,275,
- Vazdekis
- Starburst99, includes HII region contribution, i.e. emission line
fluxes
- others
- BC models try to include all stages of evolution, use observed
spectra for atmospheres at solar metallicity but models at other
metallicities. Bertelli et al have all metallicities, need to use
model atmospheres for most cases. Worthey uses older isochrones
(diff opacities), model atmospheres, appoximations for later stages
of evolution.
- Charlot, Worthey, Buzzoni paper: just from stellar physics alone, ages
are uncertain to 25-50%.
- Dependence of color and luminosity on time (
BC Fig 1) for a single
burst
- luminosity variation is combination of IMF plus rate of evolution
for lower masses.
- color evolution comes from changing mix of stellar population
- Spectral evolution (
BC Fig 4) for a variety of star formation rates.
- Note similarity of SEDs at older ages for SSPs
- Even more similar for extended SF histories
- Note potential power of UV
- dependence of contributor on wavelength (
burst (BC Fig 9)
and
constant SF rate (BC Fig 10)).
- dependence on stellar models (
Worthey 33
and
Worthey 34,
Charlot et al Fig 2).
- Even with perfect models, there's still a problem separating age and
metallicity because of similar effect of age and metallicity: the
age-metallicity degeneracy (for integrated light).
- Increasing Z makes stars cooler, as does making them older. Different
color indices all behave in the same way, so even with multiple
colors, one can't distinguish age and metallicity.
( Worthey Fig 46-49).
Worthey 3/2 law ; most indices are degenerate in age and metallicity, with
(Worthey Table 6).
- Breaking the degeneracy with
line indices, e.g. H lines + others.
- Issue: emission contamination in H
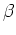 (and other indices)
(and other indices)
- This degeneracy is a problem even for a single SSP. For a
combination of SSPs the situation is worse. Here one is dominated by
the brightest contributor which may be a small contributor by mass!
- Perhaps obtaining absolute ages in this way will not be fruitful. However,
all is not lost: probably there is useful information in determining
age spread among a set of objects.
- Issues with different element abundance ratios. Note variations in
abundance ratios between solar neighborhood stars and globular clusters.


Next: Chemical evolution models
Up: AY616 class notes
Previous: Observable global properties of
Jon Holtzman
2007-05-04
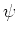 is the IMF, and
is the IMF, and 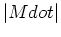 is the time
derivative of the turnoff mass.
( Renzini 1.1).
is the time
derivative of the turnoff mass.
( Renzini 1.1).
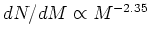 ) and
others (Pagel Fig 3).
) and
others (Pagel Fig 3).
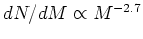 for
for 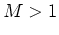 Msun,
Msun,
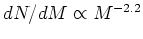 for
for 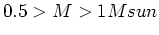 ,
,
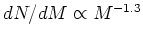 for
for 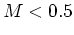 Msun.
For our purposes we'll assume that
Msun.
For our purposes we'll assume that 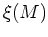 is normalized
to unit mass, i.e.,
is normalized
to unit mass, i.e.,
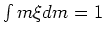 .
.
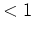 Msun).
Msun).
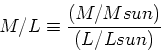
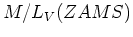
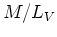
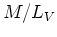
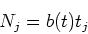
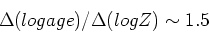
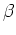 (and other indices)
(and other indices)