

Next: Spiral galaxies
Up: AY616 class notes
Previous: Stellar populations and chemical
Subsections
- Nature of ellipticals: primordial or formed by mergers? Historically,
perhaps related to discussion about origin of Milky Way halo.
- While merging is preferred in current picture of galaxy formation,
question of when the bulk of this occurred is still relevant. Lots
of very early merging may look similar to early primordial formation.
- Key issue may include to what extent merging involves stellar
systems (dry mergers) or gaseous systems (wet mergers), or what
combination.
- ellipticals come in range of colors and line strengths.
More luminous galaxies have stronger
lines/redder colors (recall slope of red sequence in abs mag vs color).
- Variation can arise either from metallicity and/or age differences
- Breaking the age-metallicity degeneracy with line indices:
Worthey Fe4668 vs H
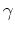 (fig 1)
suggests there is a range of ages
(fig 1)
suggests there is a range of ages
- bulk of stellar pops in E's are at least several Gyr old.
- some lower velocity dispersion galaxies appear to have lower ages
- locus of all E's suggest age spread rather than metallicity
spread.
- Absolute age dating is difficult: different results are
obtained from different indices. Some indices don't match any
models at all.
- strong evidence that there are non-solar abundance ratios,
in particular strong enhancement of Mg to Fe as compared with solar
(Worthey Fig 3).
- More luminous Es have stronger Mg overabundance than
less luminous E's. With abundance variations and lack of models and
calibration for non-solar abundance ratios, it's very to decide
about absolute ages.
- Analyis of E line strengths using atmospheres that are adjusted
for non-solar abundance ratios, and to a lesser extent, using
evolutionary tracks that apply to non-solar abundance ratios
(e.g. Trager et al. ApJ 119, 1645; ApJ 120, 165; Thomas,
Maraston, Bender).
- give much more consistent ages
(Trager fig 3),
- continue to suggest that there is a range of SSP ages among Es
(Trager fig 7).
- results of the non-solar abundance ratios are somewhat, but not
totally, expected; most alpha-elements are enhanced, but not Ca!
- some suggestion that the inferred SSP ages (remember SSP!) depend
on environment, with cluster galaxies having older ages;
current sample is not a volume limited, or in fact, rigorously
selected at all (although it tries to be ``representative'')!
- While unfortunately only based on a relatively small sample
of
 50 galaxies, some interesting correlations between
stellar population parameters.
50 galaxies, some interesting correlations between
stellar population parameters.
- the galaxies appear to lie on a plane
(Trager II. Fig 2)
in the 4-dimensional space of velocity dispersion, SSP age, SSP
metallicity, and SSP enhancement ratio.
- good correlation between velocity dispersion and enhancement ratio,
such that galaxies with higher velocity dispersion are more
``enhanced''.
- Given velocity dispersion and SSP age, SSP metallicity is
well-predicted.
- Note that these integrated light studies are luminosity-weighted, and
there exists the possibility that they are just telling us about a small
fraction (by mass) of the stellar population. ``Frosting'' models.
- Note that even if bulk of stellar ages are large, issue is still open
about whether the stars were necessarily in place in the present-day
galaxy for a very long time (e.g. late dry mergers would still show old
stellar populations).
- correlation with global properties: relation between luminosity
and line strength (which we've seen in Local Group galaxies);
- in Es, this correlation is even tighter when considering
relation between central velocity dispersion and line strength
(the
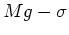 relation) (BBF.II Fig 3), over large range of
relation) (BBF.II Fig 3), over large range of 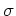 .
.
- Of equal interest to the Mg-
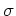 relation is the quite small
scatter around the relation.
relation is the quite small
scatter around the relation.
- has been argued that this provides strong constraint on age or
metallicity spread at any given
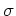 , of order 15% in
age for larger systems (but 50% in age for smaller systems),
or variations in Z of about the same amount;
, of order 15% in
age for larger systems (but 50% in age for smaller systems),
or variations in Z of about the same amount;
- however, the existence of the hyperplane mentioned above
suggests that age and metallicity are correlated to produce nearly
constant line strength at fixed
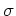 .
.
- What does all of this mean? Possible explanations for correlation
of enhancement with velocity dispersion:
- duration of star formation episode decreases at higher velocity
dispersion (most conventional interpretation)
- number of type Ia supernovae decrease at higher velocity
dispersion (origin of binaries??),
- IMF flattens at higher velocity dispersion
- Buzzoni (Fig 9) however, suggests that IMF can be
constrained using IR line strengths, and finds that galaxies
are fairly consistent with Salpeter-like IMFs, though of course,
at the current time, this only probes IMF slope of low mass stars.
- late winds are stronger at increasing velocity dispersion
(hard to understand),
- early winds are stronger with decreasing velocity dispersion.
- If most luminous ellipticals have higher metallicity and
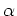 enhancement, this suggests that they cannot have been formed by the
merging of pre-existing smaller stellar systems. A significant amount of
gas must have been present from which stars were formed during/after
merger.
enhancement, this suggests that they cannot have been formed by the
merging of pre-existing smaller stellar systems. A significant amount of
gas must have been present from which stars were formed during/after
merger.
- Stellar populations within individual ellipticals: Es have
gradients in color/line strength, redder towards center
- reasonably modest, smaller than suggested by models of a single
dissipative collapse.
- Gradients might be diluted by dissipationless mergers, so
perhaps this is suggestive that such a process is important at
some level.
- Some studies find H
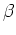 gradient suggesting that centers
of E's may be younger - but beware contamination from emission.
gradient suggesting that centers
of E's may be younger - but beware contamination from emission.
- Within a galaxy, abundance ratios of Mg and Fe are
roughly constant, as opposed to variations from galaxy to galaxy;
consistent with a global explanation for non-solar abundance ratios.
- E+A (or k+a) galaxies: galaxies with strong Balmer lines. Relatively
rare, but likely are indicative of post-starburst galaxies with significant
star formation 1 Gyr ago. (see
Goto MNRAS 357, 937, 2006)
- Not associated with cluster environment
- Some show morphological signs of recent interactions
- 3D shapes of ellipticals: oblate vs. prolate vs. triaxial.
Determine true shapes by looking at distribution of ellipticities
- distribution function is different for fainter and brighter E's.
- For bright giant E's, distribution is inconsistent with either
prolate or oblate intrinsic shapes: not enough circular galaxies
(Tremblay and Merritt Fig 3).
- fainter galaxies, however, distribution is consistent with
oblate, prolate, or triaxial.
- Triaxiality is also inferred for some giant Es from observation
of isophotal twisting, which you can't get from oblate or prolate
shape (de Zeeuw, Fig 1).
- Origins of shapes is related to dynamics of ellipticals: consider
velocities of stars in Es.
- Can measure rotation as well as velocity dispersion as function
of radius.
- Relative importance of organized over random motion can be
characterized by
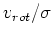 . For an oblate model with
isotropic velocity distribution which is flatted by rotation,
get
. For an oblate model with
isotropic velocity distribution which is flatted by rotation,
get
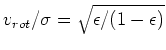 .
.
- giant Es have less rotation than this, implying anisotropic
velocity disperions.
- low luminosity (high SB) Es, however, may be isotropic with
flattening
caused by rotation (de Zeeuw Fig 3).
- low SB E's appear to have anisotropic velocity dispersion:
measured in LG E's 185 (factor of three low in
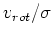 ),
147, 205 (factor of 10 low).
),
147, 205 (factor of 10 low).
- Significant fraction of ellipticals may have dynamical subcomponents,
e.g. kinematically decoupled cores (e.g.
SAURON NGC4365
- Departures from ellipses: boxy and disky isophones.
- Many ellipticals are not precisely elliptical.
- In most cases, major deviation from ellipticity is measured by the
amplitude of the
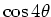 term in a given elliptical isophote.
Positive
term in a given elliptical isophote.
Positive 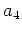 are disky, negative are boxy.
are disky, negative are boxy.
- deviations from elliptical shape is correlated with dynamics, such
that slower rotators are more likely to be boxy, and faster rotators
more likely to be disky
(Kormendy and Bender Fig 2)
- appears to be two kinds of boxiness, one found in giant Es and one
found in bulges, which in fact are relatively rapid
rotators. Likely that these come from different origins:
plausibly, mergers in the case of giant Es and bars/disk evolution
in the case of bulges.
- Possibly isophotal deviations form a continuous sequence, from S
to S0 to disky E's to true E's to boxy E's.
- also possible that true E's are just disky Es viewed
face-on (Kormendy and Bender Fig 3), and that there are two distinct classes of Es.
- Relation between shape and population. Disky galaxies are
apparently younger: is the disk an accreted population or
intrinsically different?
- Central properties: cuspy vs. core ellipticals.
- Central surface brightness profiles appear to be
bimodal.
Common representation is given by ``Nuker'' law:
- Profile type is correlated with luminosity.
Luminous ellipticals tend to have ``cuspy cores'' with a break
radius and shallower central density profile.
- Lower luminosity ellipticals have power laws all the way in.
- The core properties are correlated with the global shapes and
dynamics: cuspy core galaxies are boxy and anisotropic, cuspy
galaxies are disky and rotating.
- Black holes and BH-
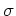 relation.
relation.
- Based on gas and stellar kinematics from high spatial resolution
observations, ellipticals harbor supermassive black holes in their
centers.
- Relation between BH mass and velocity dispersion
- Formation of ellipticals by mergers
- Idea of elliptical formation by mergers first proposed by Toomre& Toomre
- Numerical simulations (e.g. Barnes & Hernquist) show that mergers of
two roughly equal-mass stellar disks give remnants with
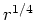 profile,
with relatively little rotation, via tidal disruption
profile,
with relatively little rotation, via tidal disruption
- Other simulations (e.g., Burkert & Naab):
- details of resultant isophotal shape depends on details of
merger, i.e. the
mass ratio of progenitors;
higher mass ratio mergers give diskier remnants.
- kinematics
also depends on mass ratio
- May be difficult to form luminous ellipticals via spiral:spiral
mergers; however, mergers of elliptical systems may be able to
reproduce these (e.g. Naab et al. ApJL 636, 81 (2006)
Fig 3)
- there is a relation between the three fundamental global observables: surface
brightness (or luminosity), size, and velocity dispersion. Original
refs: Dressler et al ApJ 313, 42, Djorgovski and Davis ApJ 313,59.
- galaxies do not populate the entire 3-space of I, r, and
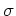 , but
instead populate only a plane in this space.
, but
instead populate only a plane in this space.
- observed relation given by Virgo ellipticals is
- called the fundamental plane
- What is the origin of this relation?
- Might expect something like this if three assumptions are true: Es are
in virial equilibrium, M/L varies systematically with luminosity, and Es
form a ``homologous'' family, all, e.g., with deVaucouleurs profiles.
- In this case, one expects
where the first relation is a definition, the second is the virial theorem,
and the constants have to do with the shapes of the galaxies.
- Combining these, we get
If one has
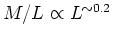 , one then recovers the observed
fundamental plane. Alternatively, one could have constant
, one then recovers the observed
fundamental plane. Alternatively, one could have constant 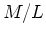 with
a structure which varies relative to one or more of the fundamental variables.
with
a structure which varies relative to one or more of the fundamental variables.
- However, still need to understand origin of assumptions:
- Why should parameters, e.g. mass-to-light, vary smoothly with
luminosity? Recall this mass-to-light includes dark matter.
- if ellipticals have dark matter halos, don't require luminous
inner parts to be in virial equilibrium
- relatively little scatter around the fundamental plane,
implying that the assumptions are reasonably valid over a large range
of elliptical properities, which implies some significant regularities in
the galaxy formation process.
- Galaxies do not fully populate the entire plane defined by our relation,
Consider the projection of the fundamental plane onto the different 2-D
spaces (Djorgovski Fig 2).
- surface brightness-
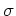 plane is presumably related to underlying
physical parameters density and virial temperature. In this plane,
can only form galaxies where cooling is effective, i.e.
at larger densities and hotter temperatures. This restricts the area in
the space in which we can find galaxies.
plane is presumably related to underlying
physical parameters density and virial temperature. In this plane,
can only form galaxies where cooling is effective, i.e.
at larger densities and hotter temperatures. This restricts the area in
the space in which we can find galaxies.
- Additional features of the galaxy formation process may introduce
additional restrictions into allowed locations of galaxies on the
fundamental plane. Most luminous ellipticals are
located along one line (with some scatter) in the fundamental plane, and
most diffuse Es are located along another.
- Consequently, when the plane is projected onto the other two axes, one
can see a correlation.
- In the luminosity(size)-
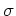 plane, one finds that
plane, one finds that
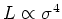 which is known as the Faber-Jackson relation;
however, since the locus of Es isn't perfectly linear and the plane
defined by the Es isn't perpendicular to this dimension, the scatter
around F-J is larger than the scatter around the FP. One can define
a new radius which incorporates surface
brightness, such that the new radius vs
which is known as the Faber-Jackson relation;
however, since the locus of Es isn't perfectly linear and the plane
defined by the Es isn't perpendicular to this dimension, the scatter
around F-J is larger than the scatter around the FP. One can define
a new radius which incorporates surface
brightness, such that the new radius vs 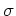 views the FP edge-on;
such a size measurement is called
views the FP edge-on;
such a size measurement is called 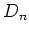 where
where 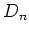 is the isophotal
diamter of the B=20.75 isophote. This
is the isophotal
diamter of the B=20.75 isophote. This 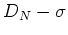 relation provides a
very useful distance estimator - if the FP is really fundamental.
relation provides a
very useful distance estimator - if the FP is really fundamental.
- In the surface brightness-size plane, one sees a relation in which
smaller galaxies have higher surface brightness for normal Es; the
diffuse Es have totally different behavior where smaller galaxies have
lower SB. These are sometimes known as the Kormendy relations, and are
one of the main bases for separating these two types of objects.
- The location of galaxies within the plane suggests important processes about
galaxy formation. For these purposes, it's convenient to designate
new axes for the 3-space within which galaxies lie, following BBF,
ApJ 399, 462. This ``
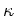 -space'', has
-space'', has
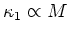 ,
,
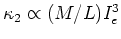 , and
, and
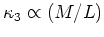 . In this space,
the fundamental plane is nearly face-on in the
. In this space,
the fundamental plane is nearly face-on in the 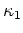 -
-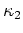 plane, and
plane, and 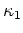 -
-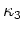 plane is edge-on to the fundamental
plane by definition. Galaxies then fall in this space according to BBF
Figures 2a/2b.
plane is edge-on to the fundamental
plane by definition. Galaxies then fall in this space according to BBF
Figures 2a/2b.
- Note that there are two apparent sequences in the fundamental plane,
one occupied by giant Es, intermediate Es, bulges, and some compact Es,
and another occupied by dwarf galaxies. There is a clear limitation
within the plane, which must have something to do with galaxy formation.
- Looking perpendicular to the plane, we find that bright dwarfs are
found systematically above the plane, which may suggest that they have
higher M/L ratios. Dwarf spheroidals are way off plane, but note that
this assumes virial equilibrium. Bulges lie below the plane, which may
be caused by lower M/L or possibly by disk contamination. Note that
anisotropic velocity dispersions are found both at low mass and at
high mass.
- Most of the physical processes which might be important in galaxy
formation/evolution move galaxies within the
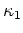 -
-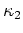 plane
(BBF Figure 4).
For example, dissipation increases surface brightness
at constant mass. Merging increases mass, possibly size depending on
model. Winds decrease mass and surface brightness; they also move points
off of the plane, possibly suggestive for dSphs. Tidal stripping makes
objects higher SB and smaller.
plane
(BBF Figure 4).
For example, dissipation increases surface brightness
at constant mass. Merging increases mass, possibly size depending on
model. Winds decrease mass and surface brightness; they also move points
off of the plane, possibly suggestive for dSphs. Tidal stripping makes
objects higher SB and smaller.
- Ideas about origin of location of galaxies in fundamental plane:
E sequence as a merging sequence, with SB declining with increasing
mass, velocity anisotropy increasing. The fact that the lower mass
Es have more rotation suggests that dissipation gets less important
as one goes to higher mass Es. Systems with rotation have higher SB.
Bulges fit in this sequence. Compact Es are like bulges, but don't have
associated disks. So the entire sequence is a merging sequence, where the
importance of gas increases as one goes towards lower mass.
- Still puzzling about Mg-
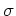 relation, however, in relatively
dissipationless merging hypothesis; however, maybe merging doesn't
increase velocity dispersion? Note that scatter around the Mg-
relation, however, in relatively
dissipationless merging hypothesis; however, maybe merging doesn't
increase velocity dispersion? Note that scatter around the Mg-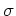 relation does not appear to be correlated with any scatter or location
in the FP.
relation does not appear to be correlated with any scatter or location
in the FP.
- On the contrary, dwarf galaxies may be more shaped by mass-loss than by
merging - but it's unclear what the progenitor galaxies are.
- What about dark matter?(see review by Gerhard 2006).
Theoretically, it is clearly expected.
- harder to observe directly than in spirals because of lack of good dynamical
tracer, e.g. a rotating component
- for non rotating components, velocity dispersion is insufficient to
measure masses because of unknown velocity anisotropy.
- potential tracers
- planetary nebulae
- globular clusters
- velocity distribution of stars
- X ray halos
- gas disks (rare, but do exist)
- from stellar velocity distributions, most elliptics show evidence
of increasing M/L as a function of radius,
indicating the presence of dark matter in the inner regions
- Has been some debate about PN observations at larger radii, with
some observations suggesting declining circular velocities. However, understanding
of velocity anisotropy is important to the conclusion
- X ray halos, when they exist, generally indicate the presence of
dark matter halos
- Finally, ellipticals have extended dark matter halos as traced
by satellite galaxies, although it requires stacking many galaxies to see
the signature(e.g., Prada et al. 2003),
and also from weak lensing studies.


Next: Spiral galaxies
Up: AY616 class notes
Previous: Stellar populations and chemical
Jon Holtzman
2007-05-04
 50 galaxies, some interesting correlations between
stellar population parameters.
50 galaxies, some interesting correlations between
stellar population parameters.
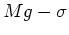 relation) (BBF.II Fig 3), over large range of
relation) (BBF.II Fig 3), over large range of 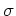 .
.
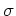 relation is the quite small
scatter around the relation.
relation is the quite small
scatter around the relation.
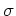 , of order 15% in
age for larger systems (but 50% in age for smaller systems),
or variations in Z of about the same amount;
, of order 15% in
age for larger systems (but 50% in age for smaller systems),
or variations in Z of about the same amount;
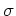 .
.
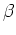 gradient suggesting that centers
of E's may be younger - but beware contamination from emission.
gradient suggesting that centers
of E's may be younger - but beware contamination from emission.
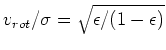 .
.