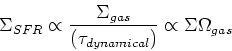

Next: Clusters and cluster galaxies
Up: AY616 class notes
Previous: Elliptical galaxies
Subsections
- same sort of global scaling relations as the fundamental plane is
observed in spiral galaxies - for spirals, the relation is that
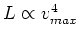 , known as the Tully-Fisher relation.
Here,
, known as the Tully-Fisher relation.
Here, 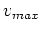 is the maximum rotation velocity observed in a spiral disk;
sometimes observed via HI line widths, and sometimes via optical rotation curves.
Note that this relation doesn't explictly include surface brightness, so
family of spirals may be even further restricted than elliptical (which fell
on a plane in 3D space of luminosity, velocity, surface brightness); however,
may partly be artifact of selecting spirals with higher SB (see more below).
is the maximum rotation velocity observed in a spiral disk;
sometimes observed via HI line widths, and sometimes via optical rotation curves.
Note that this relation doesn't explictly include surface brightness, so
family of spirals may be even further restricted than elliptical (which fell
on a plane in 3D space of luminosity, velocity, surface brightness); however,
may partly be artifact of selecting spirals with higher SB (see more below).
- naive explanation is similar to that for the fundamental plane, namely the
virial theorem. Here we have
With a bit of algebra, we derive
.
- Problems with the explanation:
- to get the TF relation, we require the process of galaxy
formation/evolution to give
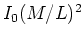 approximately constant at fixed
approximately constant at fixed
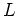 and
and 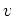 . So far, there has been no clear reason for this to occur. We know
that disk galaxies have a range of surface brightnesses and a trend of surface
brightness with luminosity. Again, this
. So far, there has been no clear reason for this to occur. We know
that disk galaxies have a range of surface brightnesses and a trend of surface
brightness with luminosity. Again, this 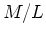 include dark matter, so it's
not just stellar populations.
include dark matter, so it's
not just stellar populations.
- Another indication that the TF relation may be more complex is that the
observed slope
of the relation is not exactly 4, and in fact, depends on the bandpass
and the nature of how the velocity is measured. The IR relation is
closest to the nominal slope, and often, this result is interpreted as
implying that extinction is important in the optical bandpasses. However,
some work has shown that the derived slope depends on the aperture
used, and the IR results are from small aperture measurements; when mags are
extrapolated to total mags, the slope becomes shallower. So the simple
explanation may not be much of an explanation.
- For most studies of the TF relation, only high SB galaxies are
considered, suggesting M/L independent of L for these. However, on
closer inspection, the TF relation shows some curvature at fainter mags.
This nonlinearity suggests that (M/L) increases at lower luminosity.
- In spirals, luminosity is not a direct tracer of mass because of differences
in stellar populations, and also in gas content. This has led to the measurement
of the baryonic TF relation. This
provides some clues about ratio of baryonic to total mass in galaxies.
- Given potentially simpler kinematics in spirals (dominated by rotation),
can trace distribution of mass, via rotation curves:
- Rotation curves probe dark matter content and profile
- general observation that rotation curves are
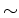 flat implies that
flat implies that
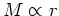 ,
,
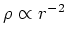 .
.
- however, shape of the rotation curve is moderately well-correlated with
the luminosity, in the sense that one gets steeper RCs for lower L galaxies
(Persic and Salucci Fig 4).
However there is significant variation at each luminosity.
- Note variety of RC shapes - there is no disk-halo conspiracy required to make
all RC flat, because all RCs aren't flat!
- Comparing rotation profile with luminosity
profile allows one to determine whether the luminous mass is able to
produce the rotation profile, and one finds that dark mass is required,
that the fraction of dark mass increases with radius, and also that the
DM fraction increases at fixed radius with decreasing luminosity.
- to determine the amount of dark matter in disk galaxies requires
knowledge about the M/L of the stellar population, which we don't know (it
depends on the star formation history).
- given luminosity profile, shapes of the RC curves tell us that DM is
there, because there's no way to get high enough stellar mass-to-light
ratios in the outer region
- can't derive the stellar M/L from the rotation
curve because of the presence of dark matter for which we don't know
the density distribution.
- common assumption is the ``maximum-disk'' hypothesis, in which one
assumes that the innermost parts of the rotation curve are driven by the
luminous mass alone - these regions then give a M/L, which is assumed
constant as a function of radius. Combined with the outer rotation curve,
mass profiles for the luminous and dark components are derived
(Kent 1a
,Kent 1b.
- However, applicability of maximum disks is debateable.
- RCs of LSB galaxies confirm the high M/L of LSB galaxies. Compare 2
galaxies at identical positions in TF relation and see that LSB galaxy
much more DM dominated (e.g. de Blok & McGaugh
Fig 3).
Universal RC might need to be 2D with SB and luminosity.
- Shapes of LSB rotation curves currently under active debate, as to
what they imply for dark matter distribution.
- Numerical models predicts cuspy distribution of dark matter, with
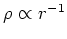 in the inner parts (Navarro-Frenk-White NFW
profile).
in the inner parts (Navarro-Frenk-White NFW
profile).
- Some observations suggest more of a core
- However, interpretation of relatively low velocities in LSB
centers can be complicated by a variety of effects, e.g.
projection, beam smearing, non-circular velocities, etc.
- want to know the star formation history of spirals
and see if they are correlated with any global properties such as Hubble
type, environment, etc.
- since we see star formation ongoing in disks, the situation is usually
interpreted in a different way than in E galaxies, where we assumed some simple
combination of SSPs was probably correct (or even a single SSP!).
Information on detailed age distributions in spirals is
quite limited; difficult in MW because of unknown distances to stars
and extinction, and difficult to probe far down the LF in M31. Note
Hipparcos results on
solar neighborhood,
and HST/ground results on the bulge.
- since SF is ongoing in spirals, it's generally assumed that it has been
ongoing since the age of the disk, and the SF history is often simply
parameterized by an exponential rate,
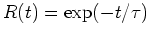 , which very
possibly is a poor representation! The exponential time scale is often
characterized by the birthrate,
, which very
possibly is a poor representation! The exponential time scale is often
characterized by the birthrate, 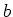 , which gives the rate of current SF
to the past SFR averaged over the age of the disk.
, which gives the rate of current SF
to the past SFR averaged over the age of the disk.
- current SF can be estimated from a variety of techniques
- H
 observations, which gives the number of ionizing photons
if one assumes that all ionizing photons are used and eventually re-emitted -
a limitation is extinction, and the assumption that HII regions are
ionization bounded.
observations, which gives the number of ionizing photons
if one assumes that all ionizing photons are used and eventually re-emitted -
a limitation is extinction, and the assumption that HII regions are
ionization bounded.
- far-IR flux (but beware heating from IS radiation field)
- radio continuum emission (beware non-thermal components)
- far-UV flux (UIT, Galex) (beware extinction)
- relation between the H
 EW and the broadband color can be used
to estimate the IMF if the exponential SFH is assumed, e.g.
Kennicutt et al Fig 2,
EW and the broadband color can be used
to estimate the IMF if the exponential SFH is assumed, e.g.
Kennicutt et al Fig 2,
- birthrate parameter can be estimated either by comparison with the
models, or more directly by using the H
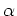 luminosity to determine
the current SFR and then estimating the past SFR by measuring the mass
of the disk. This latter involves determining a stellar M/L for the disk.
Comparison of methods (Kennicutt et al Fig 4).
luminosity to determine
the current SFR and then estimating the past SFR by measuring the mass
of the disk. This latter involves determining a stellar M/L for the disk.
Comparison of methods (Kennicutt et al Fig 4).
- mild indication that the IMF of high-mass stars in external galaxies
appears to be somewhat shallower than that of our own galaxy
but the uncertainties/assuptions in the method may lead to substantial
systematic problems.
- Results suggest systematic variation of star formation history with
Hubble type (Kennicutt et al Fig 6); but note classification issues.
- metallicities of spirals: present Z distribution derived from ISM. Stellar
distribution harder to determine - complicated by age and extinction
effects (see Gallazzi et al MNRAS 362, 41 (2005)).
- Present day metallicities are correlated with galaxy luminosity,
e. g. Tremonti et al ApJ 613, 898 (2004),
Fig 4
- Correlation even clearer with
stellar mass
- Probably not just due to slower evolution at lower masses (i.e. closed
box model), but to mass loss in lower mass galaxies
- Similar trends seen in
stellar metallicities and ages, albeit with larger scatter (some from
observational technique)
- Gradients appear to exist, but do not seem be to well correlated
with anything (gradients flatter in more luminous galaxies??)
- Spirals provide a good laboratory to study processes which affect star
formation. Especially important given lack of understanding of star
formation; galaxy formation models need to parameterize it.
- Star formation rates vary significantly from galaxy to galaxy.
- Strongly star forming galaxies called starburst galaxies
- Very strongly star forming galaxies often produce high ratio of far-IR
radiation to optical radiation, and are called ultra-luminous infrared
galaxies (ULIRGs)
- Is SFR correlated with amount of gas in galaxy? When normalized by galaxy
mass, find good correlation with HI mass, but poor correlation with CO
(Kennicut Fig 3).
This is peculiar; possible explanation include real
lack of correlation with molecular content, or variations in conversion
factor from CO to
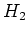 , or importance of local distribution.
, or importance of local distribution.
- Distribution of gas within spirals: molecular gas more centrally
concentrated. In some galaxies, CO traces H
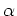 well, but not in others
(Kennicut figs 4
and 6).
H
well, but not in others
(Kennicut figs 4
and 6).
H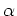 in general traces CO better than it traces
HI, in contradiction to the global properties. In general, it seems
that SF is more directly coupled to total gas density, atomic+molecular,
rather than to any particular phase. Note that SF essentially shuts off
in outer regions of disk, even though there's plenty of gas there.
in general traces CO better than it traces
HI, in contradiction to the global properties. In general, it seems
that SF is more directly coupled to total gas density, atomic+molecular,
rather than to any particular phase. Note that SF essentially shuts off
in outer regions of disk, even though there's plenty of gas there.
- Star formation laws.
- Schmidt law, which has
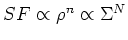 .
.
- Measured relations show a more complex behavior
(Kennicutt Fig 8).
- slope in regions of high gas density roughly comparable between
galaxies (Schmidt law), but different galaxies have different thresholds for SF.
Kennicutt SF law.
- threshold
density is expected from consideration of stability of disks - below
critical density, disks are stable against large scale perturbations;
for a thin isothermal gas disk,
 , where
, where 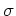 is the gas velocity disperions, and
is the gas velocity disperions, and 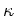 is the epicyclic frequency, which is related to the rotation curve. The
critical density depends on rotation profile and velocity dispersion.
is the epicyclic frequency, which is related to the rotation curve. The
critical density depends on rotation profile and velocity dispersion.
- density of gas in spirals matches reasonably well the profile
of critical density
(Figs 10
& 11).
In this model, the threshold surface density is a function of radius
(Fig 14).
Suggests threshold as f(r)
then Schmidt law with
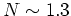 - with several possible systematic
uncertainties (extinction, other factors which vary with r). However,
behavior near the threshold is significantly steeper - and most regions
of most galaxies appear to be near the threshhold!
- with several possible systematic
uncertainties (extinction, other factors which vary with r). However,
behavior near the threshold is significantly steeper - and most regions
of most galaxies appear to be near the threshhold!
- global star formation law. Star forming galaxies show range of current
star formation rates from
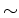 1 Msun/yr to hundreds of Msun/yr; what sets the SFR?
Results from a sample of
normal galaxies (Kennicutt Fig 2),
starburst galaxies(Kennicutt Fig 5),
and all galaxies combined (Fig 6).
Remarkably tight relation is seen over wide range of densities and star formation rates.
1 Msun/yr to hundreds of Msun/yr; what sets the SFR?
Results from a sample of
normal galaxies (Kennicutt Fig 2),
starburst galaxies(Kennicutt Fig 5),
and all galaxies combined (Fig 6).
Remarkably tight relation is seen over wide range of densities and star formation rates.
- multiple explanations may give observed trend: consider two possible qualitative
physical mechanisms behind observed relations.
- star formation related to growth of instabilities suggests
- Alternatively, perhaps SF is related to the local dynamical
timescale (e.g., SF triggered by passage through spiral arms). Then
- Both give comparable SFRs (Kennicutt Figure 7).
- gas consumption ``paradox"
- Mean time given by
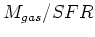 (e.g. Kennicut et al Fig 7).
(e.g. Kennicut et al Fig 7).
- Possible resolutions:
- Possibly resolved by considering recycling.
- Missing gas-rich galaxies? Low SB galaxies may resolve the apparent
paradox, since these have very high gas mass fractions. It appears that the
gas fraction is correlated with the SB
(McGaugh and de blok fig 1).
Given significant numbers of LSB galaxies, paradox is resolved. LSBs as
``retarded" galaxies
- Stars form from ISM, but also influence the structure of the ISM in
return.
- ISM is a multi-phase medium, with molecular clouds, cold atomic gas,
diffuse ionized gas, HII regions, hot coronal gas; distribution of gas in the
ISM is notably chaotic. Often, ``three-phase medium'' (cold, warm, hot) is
discussed. Gas is not uniformly distributed, and the different phases are
interspersed with each other.
- some effect of stars on the ISM is expected from the processes of
supernovae and mass loss from stars.
- supernovae clear out ``superbubbles'' in the ISM; it is possible
that these superbubbles even propagate to the vertical edges
of the disks and allow for mass outflow from the disk into the
halo. If this is the case, one might expect this gas to eventually
fall back down onto the disk, leading the the ideas of
galactic fountains and chimneys.
- also possible that the shocks from supernovae act to compress gas
clouds, possibly trigering further star formation in nearby regions.
- Significant galactic winds (outflows) are observed in starburst galaxies,
e.g. M82
- These processes are important for understanding:
- feedback mechanisms by which star formation may be self-regulating
- chemical evolution of galactic disks
- the existence of gas halos around galaxies
- the escape of ionizing radiation from galactic disks.
- Additional feedback may come from activity in nucleii of galaxies.
This has recently become popular for considering the
comparison of model mass functions and observed luminosity
functions
for high luminosity galaxies.
- Quick AGN review (see book by Peterson, 1997)
- Seyfert galaxies: types 1 (broad lines) and 2 (narrow lines)
- BL Lac objects
- LINERS
- QSOs/quasars
- Radio galaxies.
- Energy source may be same, but don't generally directly see nuclear
activity.
- Fanaroff-Riley (FR) types 1 (low radio luminosity, edge-darkened) and
2 (high radio luminosity, edge-brightened).
- Frequency of Seyfert phenomenon; 1-2% but all(?) galaxies may harbor
activity at some level.
- Generally considered to be powered by accretion onto nuclear black hole.
Arguments for existence of BH:
- timing arguments,
- broad Fe line (see review by Fabian).
- BH masses from reverberation mapping, and comparison with
dynamical measurements of BH masses.
- Unified model;
physical picture and differences as a function of viewing
geometry. Accretion rates and accretion rate
differences (review by Pogge?). Differences from variations in
gas supply (quantity and/or efficiency of infall) and/or from different
BH masses?
- Current idea that feedback from AGN may be important in limiting
masses/luminosities of most massive galaxies
- Understanding bulges may be important in understanding nature of Hubble sequence
- Structural properties of bulges:
- Stellar population properties of bulges:
- Recall MW bulge (and halo) thought to be primarily old
(bulge CMD
and
LF); M31 halo may
be younger (Brown et al results).
- Mg-
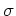 relation similar to that of ellipticals and
corresponding implications for early bulge formation.
relation similar to that of ellipticals and
corresponding implications for early bulge formation.
- Colors: Peletier and Balcells observations
(Fig 2)
of similar disk and bulge colors
- Stellar populations from line strengths
- Kinematical properties of bulges: variation of degree of rotational
support, but generally more rotational support than ellipticals
- Formation possibilities:
- monolithic collapse
- secular evolution; pseudobulges
- minor mergers, major mergers (before disk formation).
- Plausibly two (or more?) formation mechanisms for bulges.


Next: Clusters and cluster galaxies
Up: AY616 class notes
Previous: Elliptical galaxies
Jon Holtzman
2007-05-04
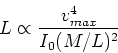
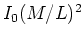 approximately constant at fixed
approximately constant at fixed
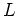 and
and 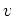 . So far, there has been no clear reason for this to occur. We know
that disk galaxies have a range of surface brightnesses and a trend of surface
brightness with luminosity. Again, this
. So far, there has been no clear reason for this to occur. We know
that disk galaxies have a range of surface brightnesses and a trend of surface
brightness with luminosity. Again, this 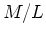 include dark matter, so it's
not just stellar populations.
include dark matter, so it's
not just stellar populations.
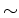 flat implies that
flat implies that
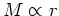 ,
,
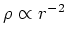 .
.
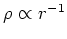 in the inner parts (Navarro-Frenk-White NFW
profile).
in the inner parts (Navarro-Frenk-White NFW
profile).